Sorting Algorithms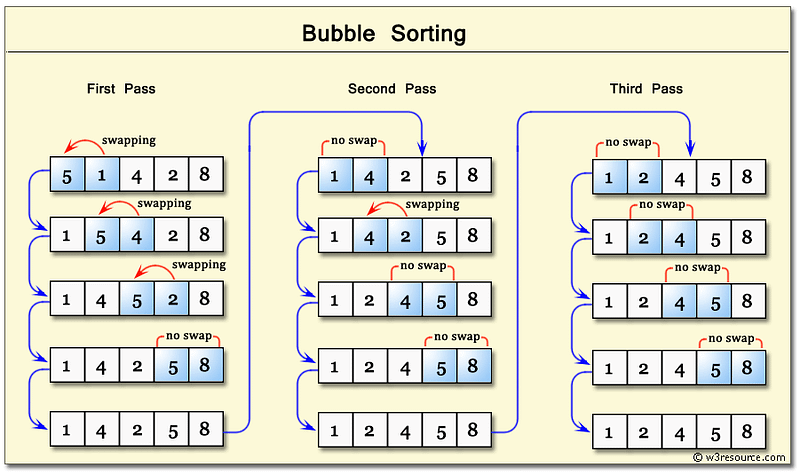

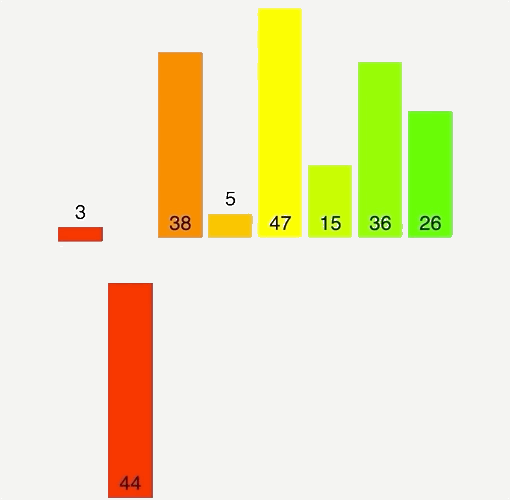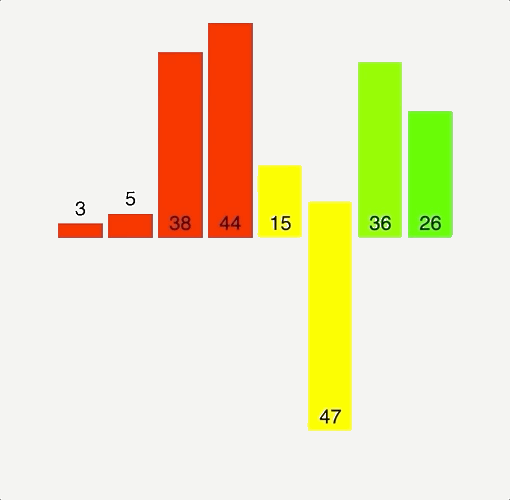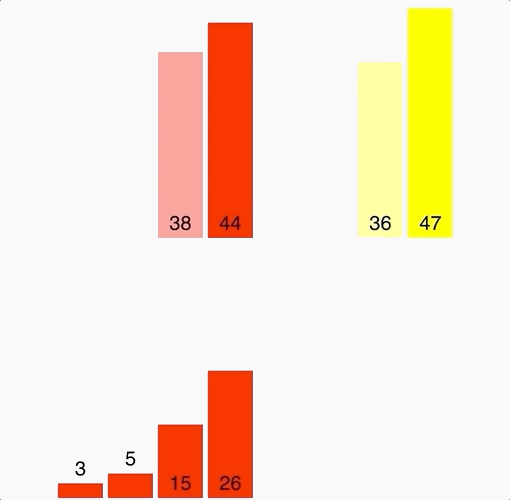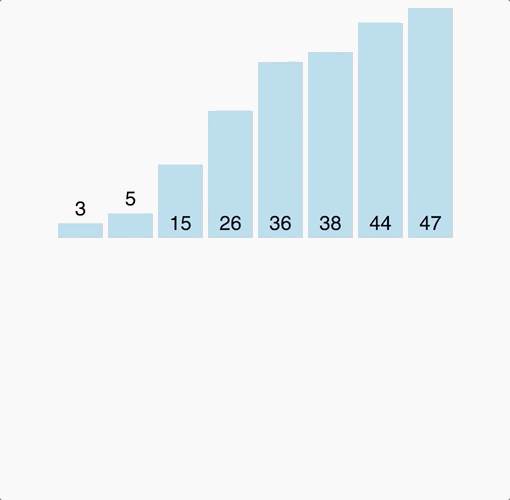
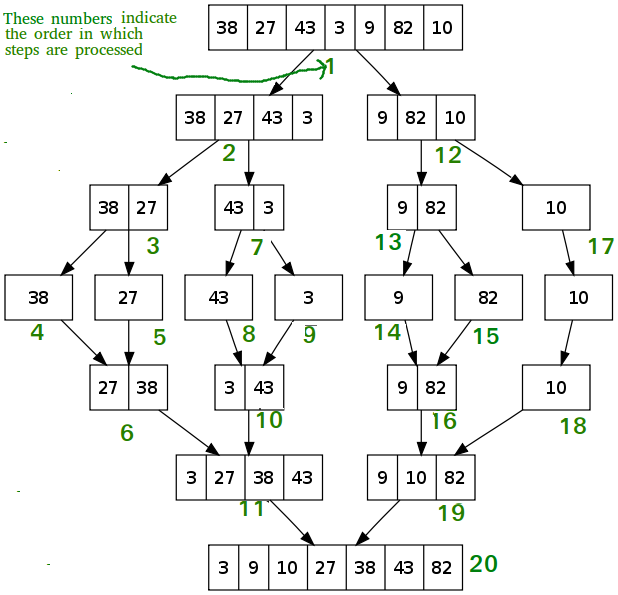
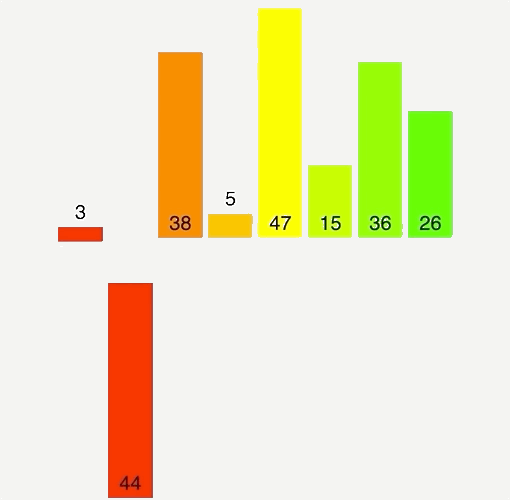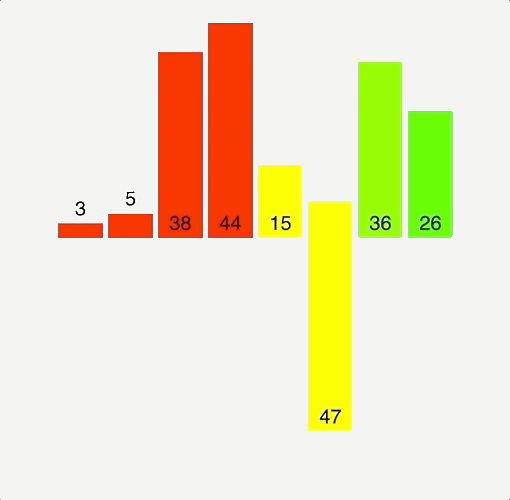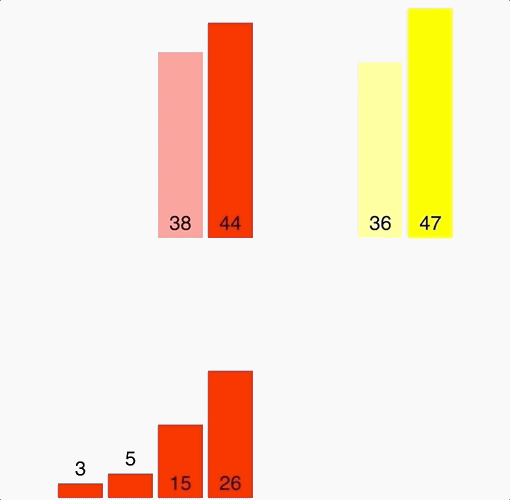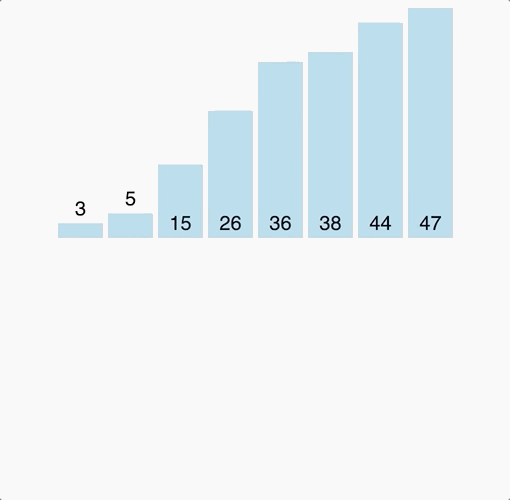
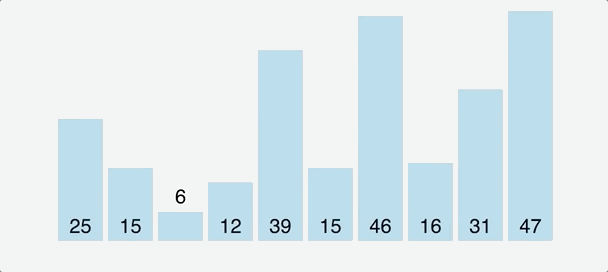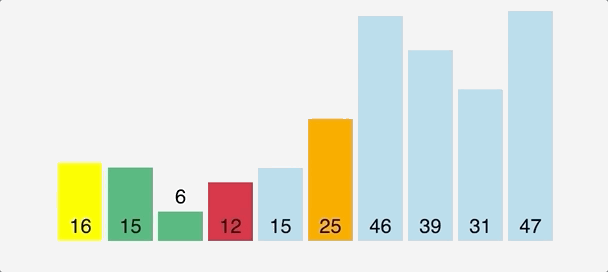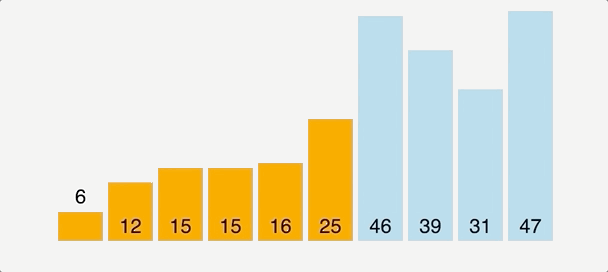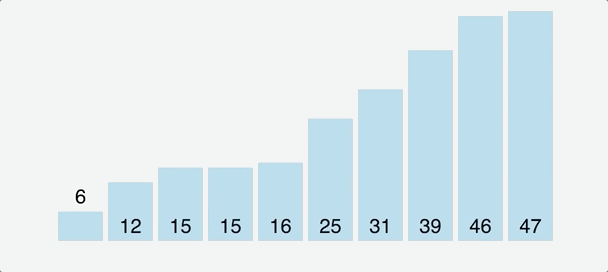
Bubble Sort
Time Complexity: Quadratic O(n^2)
- The inner for-loop contributes to O(n), however in a worst case scenario the while loop will need to run n times before bringing all n elements to their final resting spot.
Space Complexity: O(1)
- Bubble Sort will always use the same amount of memory regardless of n.
https://gist.github.com/eengineergz/e67e56bed7c5a20a54851867ba5efef6
- The first major sorting algorithm one learns in introductory programming courses.
- Gives an intro on how to convert unsorted data into sorted data.
It's almost never used in production code because:
- It's not efficient
- It's not commonly used
- There is stigma attached to it
- Bubbling Up : Term that infers that an item is in motion, moving in some direction, and has some final resting destination.
- Bubble sort, sorts an array of integers by bubbling the largest integer to the top.
https://gist.github.com/eengineergz/fd4acc0c89033bd219ebf9d3ec40b053https://gist.github.com/eengineergz/80934783c628c70ac2a5a48119a82d54
- Worst Case & Best Case are always the same because it makes nested loops.
- Double for loops are polynomial time complexity or more specifically in this case Quadratic (Big O) of: O(n²)
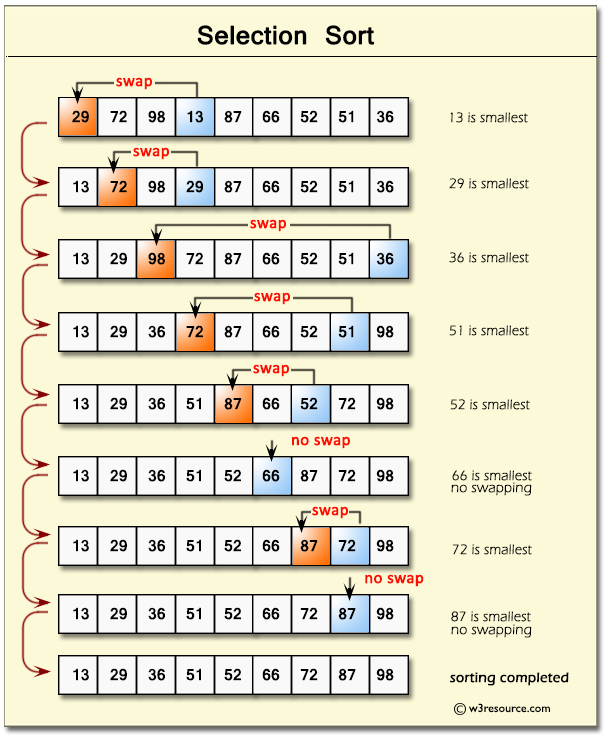
Selection Sort
Time Complexity: Quadratic O(n^2)
- Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);
Space Complexity: O(1)
- Selection Sort will always use the same amount of memory regardless of n.
https://gist.github.com/eengineergz/4abc0fe0bf01599b0c4104b0ba633402
- Selection sort organizes the smallest elements to the start of the array.
Summary of how Selection Sort should work:
- Set MIN to location 0
- Search the minimum element in the list.
- Swap with value at location Min
- Increment Min to point to next element.
- Repeat until list is sorted.
https://gist.github.com/eengineergz/61f130c8e0097572ed908fe2629bdee0
Insertion Sort
Time Complexity: Quadratic O(n^2)
- Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);
Space Complexity: O(n)
- Because we are creating a subArray for each element in the original input, our Space Comlexity becomes linear.
https://gist.github.com/eengineergz/a9f4b8596c7546ac92746db659186d8c
Merge Sort
Time Complexity: Log Linear O(nlog(n))
- Since our array gets split in half every single time we contribute O(log(n)). The while loop contained in our helper merge function contributes O(n) therefore our time complexity is O(nlog(n)); Space Complexity: O(n)
- We are linear O(n) time because we are creating subArrays.
Example of Merge Sort
https://gist.github.com/eengineergz/18fbb7edc9f5c4820ccfcecacf3c5e48https://gist.github.com/eengineergz/cbb533137a7f957d3bc4077395c1ff64
- Merge sort is O(nlog(n)) time.
- We need a function for merging and a function for sorting.
Steps:
- If there is only one element in the list, it is already sorted; return the array.
- Otherwise, divide the list recursively into two halves until it can no longer be divided.
- Merge the smallest lists into new list in a sorted order.
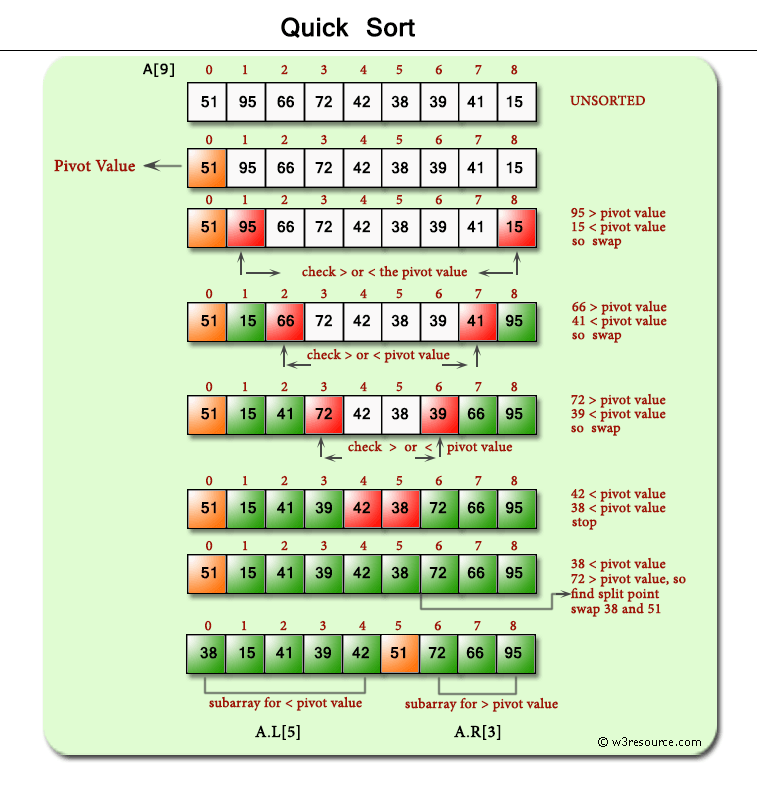
Quick Sort
Time Complexity: Quadratic O(n^2)
- Even though the average time complexity O(nLog(n)), the worst case scenario is always quadratic.
Space Complexity: O(n)
- Our space complexity is linear O(n) because of the partition arrays we create.
- QS is another Divide and Conquer
- Some key ideas to keep in mind:
- It is easy to sort elements of an array relative to a particular target value.
- An array of 0 or 1 elements is already trivially sorted.
https://gist.github.com/eengineergz/24bcbc5248a8c4e1671945e9512da57e
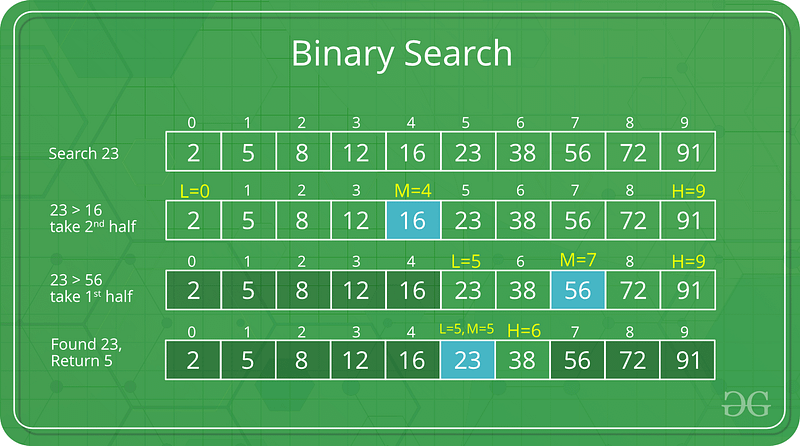
Binary Search
Time Complexity: Log Time O(log(n))
Space Complexity: O(1)
Recursive Solution
https://gist.github.com/eengineergz/c82c00a4bcba4b69b7d326d6cad3ac8c
Min Max Solution
https://gist.github.com/eengineergz/eb8d1e1684db15cc2c8af28e13f38751https://gist.github.com/eengineergz/bc3f576b9795ccef12a108e36f9f820a
- Must be conducted on a sorted array.
- Binary search is logarithmic time, not exponential b/c n is cut down by two, not growing.
- Binary Search is part of Divide and Conquer.
Insertion Sort
- Works by building a larger and larger sorted region at the left-most end of the array.
Steps:
- If it is the first element, and it is already sorted; return 1.
- Pick next element.
- Compare with all elements in the sorted sub list
- Shift all the elements in the sorted sub list that is greater than the value to be sorted.
- Insert the value
- Repeat until list is sorted.
https://gist.github.com/eengineergz/ffead1de0836c4bcc6445780a604f617
