A Quick Guide to Big-O Notation, Memoization, Tabulation, and Sorting Algorithms by Example
- Why is looking at runtime not a reliable method of calculating time complexity?
- Not all computers are made equal( some may be stronger and therefore boost our runtime speed )
- How many background processes ran concurrently with our program that was being tested?
- We also need to ask if our code remains performant if we increase the size of the input.
The real question we need to answering is:
How does our performance scale?.
big 'O' notation
- Big O Notation is a tool for describing the efficiency of algorithms with respect to the size of the input arguments.
- Since we use mathematical functions in Big-O, there are a few big picture ideas that we'll want to keep in mind:
- The function should be defined by the size of the input.
SmallerBig O is better (lower time complexity)- Big O is used to describe the worst case scenario.
- Big O is simplified to show only its most dominant mathematical term.
Simplifying Math Terms
- We can use the following rules to simplify the our Big O functions:
Simplify Products: If the function is a product of many terms, we drop the terms that don't depend on n.Simplify Sums: If the function is a sum of many terms, we drop the non-dominant terms.n: size of the inputT(f): unsimplified math functionO(f): simplified math function.
Putting it all together

- First we apply the product rule to drop all constants.
- Then we apply the sum rule to select the single most dominant term.
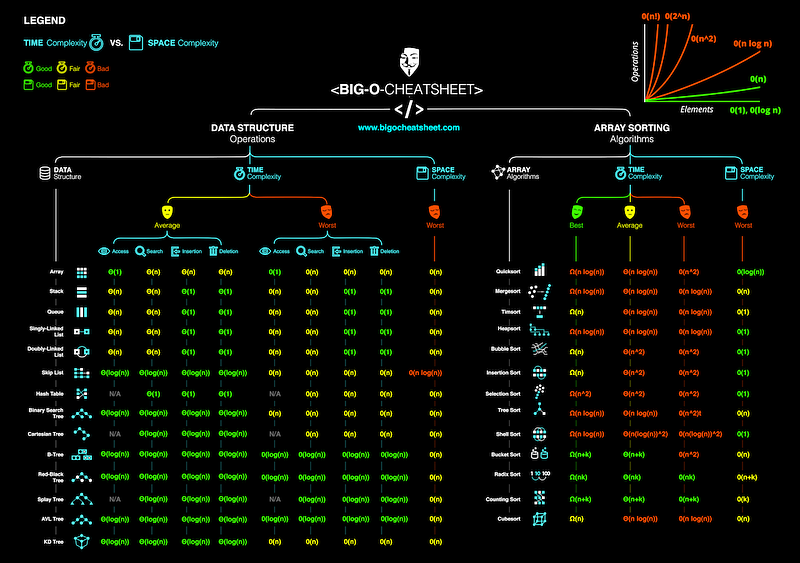
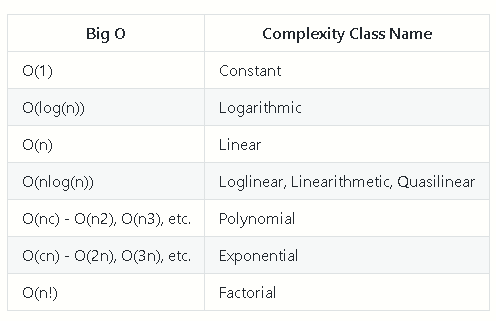
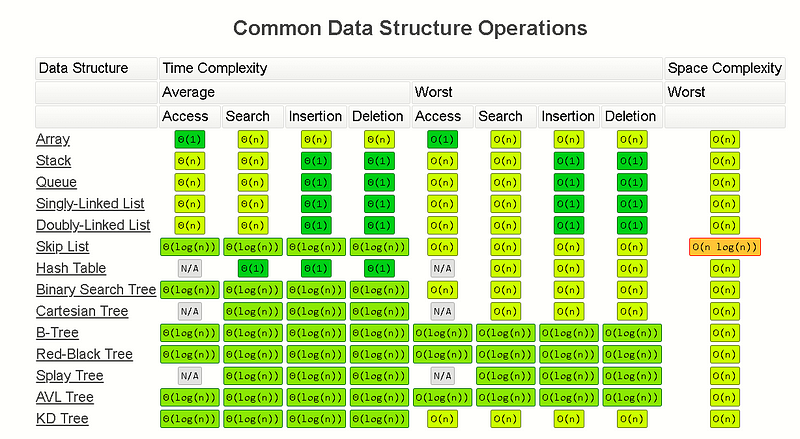
Complexity Classes
Common Complexity Classes
There are 7 major classes in Time Complexity
O(1) Constant
The algorithm takes roughly the same number of steps for any input size.
O(log(n)) Logarithmic
In most cases our hidden base of Logarithmic time is 2, log complexity algorithm's will typically display 'halving' the size of the input (like binary search!)
// O(log(n))
function logarithmic1(n) {
if (n <= 1) return;
logarithmic1(n / 2);
}
// O(log(n))
function logarithmic2(n) {
let i = n;
while (i > 1) {
i /= 2;
}
}
view rawlogorithmic.js hosted with ❤ by GitHub
O(n) Linear
Linear algorithm's will access each item of the input "once".
// O(n)
function linear1(n) {
for (let i = 1; i <= n; i++) {
console.log(i);
}
}
// O(n), where n is the length of the array
function linear2(array) {
for (let i = 0; i < array.length; i++) {
console.log(i);
}
}
// O(n)
function linear3(n) {
if (n === 1) return;
linear3(n - 1);
}
view rawlinear.js hosted with ❤ by GitHub
O(nlog(n)) Log Linear Time
Combination of linear and logarithmic behavior, we will see features from both classes.
Algorithm's that are log-linear will use** both recursion AND iteration.**
// O(n * log(n))
function loglinear(n) {
if (n <= 1) return;
for (let i = 1; i <= n; i++) {
console.log(i);
}
loglinear(n / 2);
loglinear(n / 2);
}
view rawloglin.js hosted with ❤ by GitHub
O(nc) Polynomial
C is a fixed constant. `
// O(n^2)
function quadratic(n) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {}
}
}
//Example of Quadratic and Cubic runtime.
// O(n^3)
function cubic(n) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
for (let k = 1; k <= n; k++) {}
}
}
}
view rawpoly.js hosted with ❤ by GitHub
O(c^n) Exponential
C is now the number of recursive calls made in each stack frame.
Algorithm's with exponential time are VERY SLOW.
// O(2^n)
function exponential2n(n) {
if (n === 1) return;
exponential_2n(n - 1);
exponential_2n(n - 1);
}
// O(3^n)
function exponential3n(n) {
if (n === 0) return;
exponential_3n(n - 1);
exponential_3n(n - 1);
exponential_3n(n - 1);
}
view rawexponential.js hosted with ❤ by GitHub
Memoization
- Memoization : a design pattern used to reduce the overall number of calculations that can occur in algorithms that use recursive strategies to solve.
- MZ stores the results of the sub-problems in some other data structure, so that we can avoid duplicate calculations and only 'solve' each problem once.
- Two features that comprise memoization:
- FUNCTION MUST BE RECURSIVE.
- Our additional Data Structure is usually an object (we refer to it as our memo... or sometimes cache!)


Memoizing Factorial
Our memo object is mapping out our arguments of factorial to it's return value.
- Keep in mind we didn't improve the speed of our algorithm.
Memoizing Fibonacci
- Our time complexity for Fibonacci goes from O(2^n) to O(n) after applying memoization.
The Memoization Formula
Rules:
- Write the unoptimized brute force recursion (make sure it works);
- Add memo object as an additional argument .
- Add a base case condition that returns the stored value if the function's argument is in the memo.
- Before returning the result of the recursive case, store it in the memo as a value and make the function's argument it's key.
Things to remember
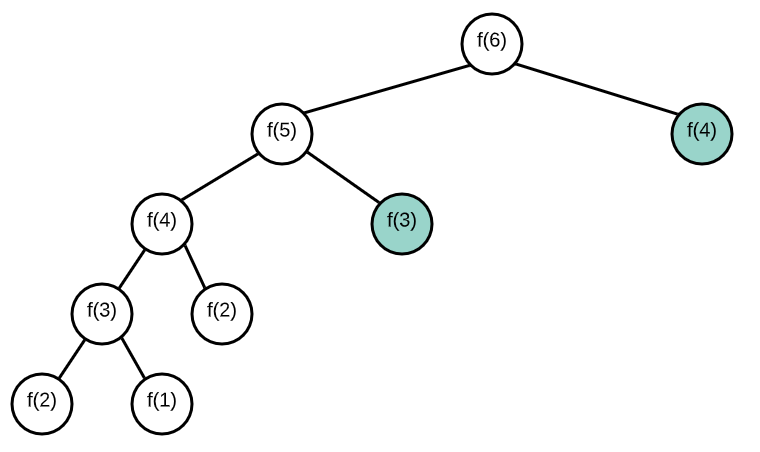
- When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
- When you notice duplicate sub-tree's that means we can memoize.
function fastFib(n, memo = {}) {
if (n in memo) return memo[n];
if (n === 1 || n === 2) return 1;
memo[n] = fastFib(n - 1, memo) + fastFib(n - 2, memo);
return memo[n];
}
fastFib(6); // => 8
fastFib(50); // => 12586269025 |
view rawfastfib.js hosted with ❤ by GitHub
Tabulation
Tabulation Strategy
Use When:
- The function is iterative and not recursive.
- The accompanying DS is usually an array.
function fib(n) {
let mostRecentCalcs = [0, 1];
if (n === 0) return mostRecentCalcs[0];
for (let i = 2; i <= n; i++) {
const [secondLast, last] = mostRecentCalcs;
mostRecentCalcs = [last, secondLast + last];
}
return mostRecentCalcs[1];
} |
view rawtabfib.js hosted with ❤ by GitHub
Steps for tabulation
- Create a table array based off the size of the input.
- Initialize some values in the table to 'answer' the trivially small subproblem.
- Iterate through the array and fill in the remaining entries.
- Your final answer is usually the last entry in the table.
Memo and Tab Demo with Fibonacci
Normal Recursive Fibonacci
function fibonacci(n) {
if (n <= 2) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
Memoization Fibonacci 1
function fibMemo(n, memo = { 0: 0, 1: 1 }) {
if (n in memo) return memo[n];
memo[n] = fibMemo(n - 1) + fibMemo(n - 2);
return memo[n];
} |
view rawfib-memo.js hosted with ❤ by GitHub
Memoization Fibonacci 2
function fib(n, memo) {
memo = memo || {};
if (memo[n]) return memo[n];
if (n <= 2) return 1;
return (memo[n] = fib(n - 1, memo) + fib(n - 2, memo));
} |
view rawmemo-fib2.js hosted with ❤ by GitHub
Tabulated Fibonacci
function tabFib(n) {
let table = new Array(n);
table[0] = 0;
table[1] = 1;
table[2] = 1;
for (i = 3; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2];
console.log(table);
}
return table[n];
} |
view rawtabfib.js hosted with ❤ by GitHub
Example of Linear Search
function search(array, term) {
for (let i = 0; i < array.length; i++) {
if (array[i] === term) {
return i;
}
}
return -1;
} |
view rawlinsearch.js hosted with ❤ by GitHub
- Worst Case Scenario: The term does not even exist in the array.
- Meaning: If it doesn't exist then our for loop would run until the end therefore making our time complexity O(n).
Sorting Algorithms
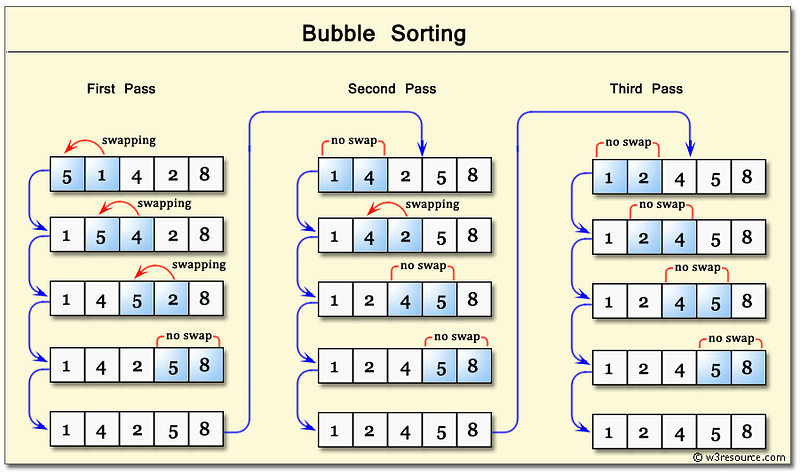
Bubble Sort
Time Complexity: Quadratic O(n^2)
- The inner for-loop contributes to O(n), however in a worst case scenario the while loop will need to run n times before bringing all n elements to their final resting spot.
Space Complexity: O(1)
- Bubble Sort will always use the same amount of memory regardless of n.
function swap(array, idx1, idx2) {
[array[idx1], array[idx2]] = [array[idx2], array[idx1]];
}
function bubbleSort(array) {
let swapped = false;
while (!swapped) {
swapped = true;
for (let i = 0; i < array.length; i++) {
if (array[i] > array[i + 1]) {
swap(array, i, i + 1);
swapped = false;
}
}
}
return array;
}
//Alt SLN-------------------------------------------------
function bubbleSort(array) {
let sorted = false;
while (!sorted) {
sorted = true;
for (let i = 0; i < array.length; i++) {
if (array[i] > array[i + 1]) {
let temp = arr[i];
array[i] = array[i + 1];
array[i + 1] = temp;
sorted = false;
}
}
}
return array;
} |
view rawbub2.js hosted with ❤ by GitHub
- The first major sorting algorithm one learns in introductory programming courses.
- Gives an intro on how to convert unsorted data into sorted data.
It's almost never used in production code because:
- It's not efficient
- It's not commonly used
- There is stigma attached to it
*Bubbling Up*_ : Term that infers that an item is in motion, moving in some direction, and has some final resting destination._- Bubble sort, sorts an array of integers by bubbling the largest integer to the top.
// Bubble Sort
function bubble(array) {
let sorted = true;
for (let i = 0; i < array.length; i++) {
let num1 = array[i];
let num2 = array[i + 1];
if (num1 > num2) {
array[i + 1] = num1;
array[i] = num2;
sorted = false;
}
}
if (sorted) {
return array;
} else {
return bubble(array);
}
} |
view rawbub.js hosted with ❤ by GitHub
function bubbleSort(items) {
let length = items.length;
for (let i = 0; i < length; i++) {
for (let j = 0; j < length - i - 1; j++) {
if (items[j] > items[j + 1]) {
let tmp = items[j];
items[j] = items[j + 1];
items[j + 1] = tmp;
}
}
}
} |
view rawbubble.js hosted with ❤ by GitHub
- Worst Case & Best Case are always the same because it makes nested loops.
- Double for loops are polynomial time complexity or more specifically in this case Quadratic (Big O) of: O(n²)
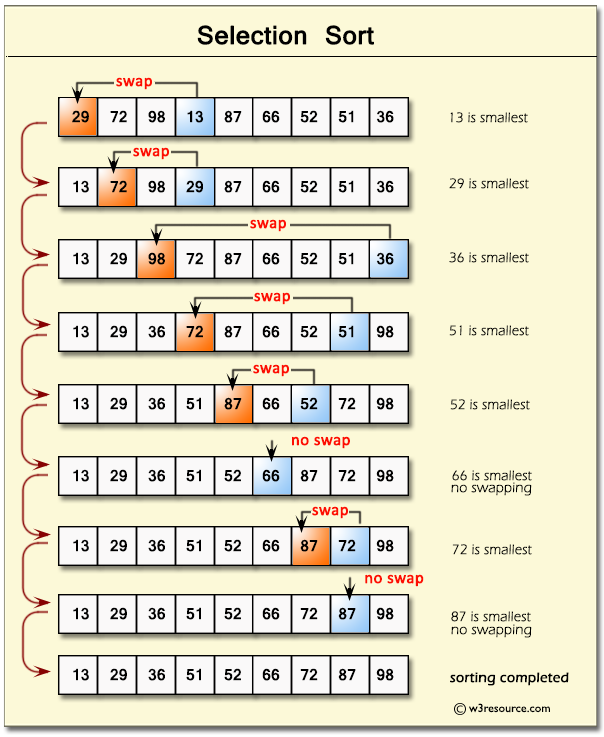
Selection Sort
Time Complexity: Quadratic O(n^2)
- Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);
Space Complexity: O(1)
- Selection Sort will always use the same amount of memory regardless of n.
function swap(array, idx1, idx2) {
[array[idx1], array[idx2]] = [array[idx2], array[idx2]];
}
function selectionSort(array) {
for (let i = 0; i < array.length; i++) {
let lowest = i;
for (let j = i + 1; j < array.length; j++) {
if (list[j] < list[lowest]) {
lowest = j;
}
}
if (place !== i) {
swap(array, i, lowest);
}
}
}
//Alt Solution----------------------------------------------------
function selectionSort(array) {
for (let i = 0; i < array.length; i++) {
let lowest = i;
for (let j = 0; j < array.length; j++) {
if (array[j] < array[i]) {
lowest = j;
}
}
if (lowest !== i) {
let temp = array[i];
array[i] = array[lowest];
array[lowest] = temp;
}
}
return array;
} |
view rawselectionsort.js hosted with ❤ by GitHub
- Selection sort organizes the smallest elements to the start of the array.
Summary of how Selection Sort should work:
- Set MIN to location 0
- Search the minimum element in the list.
- Swap with value at location Min
- Increment Min to point to next element.
- Repeat until list is sorted.
let selectionSort = (arr) => {
let len = arr.length;
for (let i = 0; i < len; i++) {
let min = i;
for (let j = i + 1; j < len; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
if (min !== i) {
let tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
return arr;
}; |
view rawselectsort.js hosted with ❤ by GitHub
Insertion Sort
Time Complexity: Quadratic O(n^2)
- Our outer loop will contribute O(n) while the inner loop will contribute O(n / 2) on average. Because our loops are nested we will get O(n²);
Space Complexity: O(n)
- Because we are creating a subArray for each element in the original input, our Space Comlexity becomes linear.
function insertionSort(array) {
for (let i = 1; i < array.length; i++) {
let value = list[i];
let hole = i;
while (hole > 0 && list[hole - 1] > value) {
list[hole] = list[hole - 1];
hole--;
}
list[hole] = value;
}
return array;
}
//Alt Solution--------------------------------------------
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let current = arr[i];
let j = i - 1;
while (j > -1 && current < arr[j]) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
return arr;
} |
view rawinsertionsort.js hosted with ❤ by GitHub
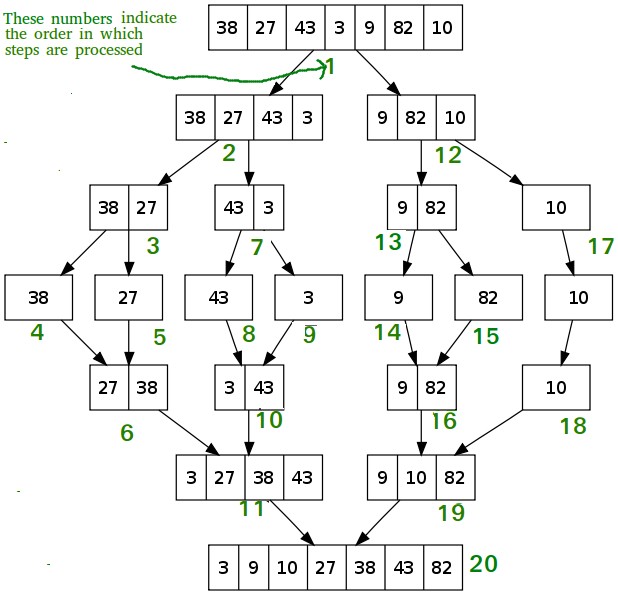
Merge Sort
Time Complexity: Log Linear O(nlog(n))
- Since our array gets split in half every single time we contribute O(log(n)). The while loop contained in our helper merge function contributes O(n) therefore our time complexity is O(nlog(n));
Space Complexity: O(n) - We are linear O(n) time because we are creating subArrays.
Example of Merge Sort
function merge(leftArray, rightArray) {
const sorted = [];
while (letArray.length > 0 && rightArray.length > 0) {
const leftItem = leftArray[0];
const rightItem = rightArray[0];
if (leftItem > rightItem) {
sorted.push(rightItem);
rightArray.shift();
} else {
sorted.push(leftItem);
leftArray.shift();
}
}
while (leftArray.length !== 0) {
const value = leftArray.shift();
sorted.push(value);
}
while (rightArray.length !== 0) {
const value = rightArray.shift();
sorted.push(value);
}
return sorted;
}
function mergeSort(array) {
const length = array.length;
if (length === 1) {
return array;
}
const middleIndex = Math.ceil(length / 2);
const leftArray = array.slice(0, middleIndex);
const rightArray = array.slice(middleIndex, length);
leftArray = mergeSort(leftArray);
rightArray = mergeSort(rightArray);
return merge(leftArray, rightArray);
} |
view rawmergesort.js hosted with ❤ by GitHub
function merge(arr1, arr2) {
let result = [];
while (arr1.length && arr2.length) {
if (arr1[0] < arr2[0]) {
result.push(arr1.shift());
} else {
result.push(arr2.shift());
}
}
return [...result, ...arr1, ...arr2];
}
function mergeSort(arr) {
if (arr.length <= 1) return arr;
const mid = Math.floor(arr.length / 2);
const left = mergeSort(arr.slice(0, mid));
const right = mergeSort(arr.slice(mid));
return merge(left, right);
} |
view rawmerge2.js hosted with ❤ by GitHub
- Merge sort is O(nlog(n)) time.
- We need a function for merging and a function for sorting.
Steps:
- If there is only one element in the list, it is already sorted; return the array.
- Otherwise, divide the list recursively into two halves until it can no longer be divided.
- Merge the smallest lists into new list in a sorted order.
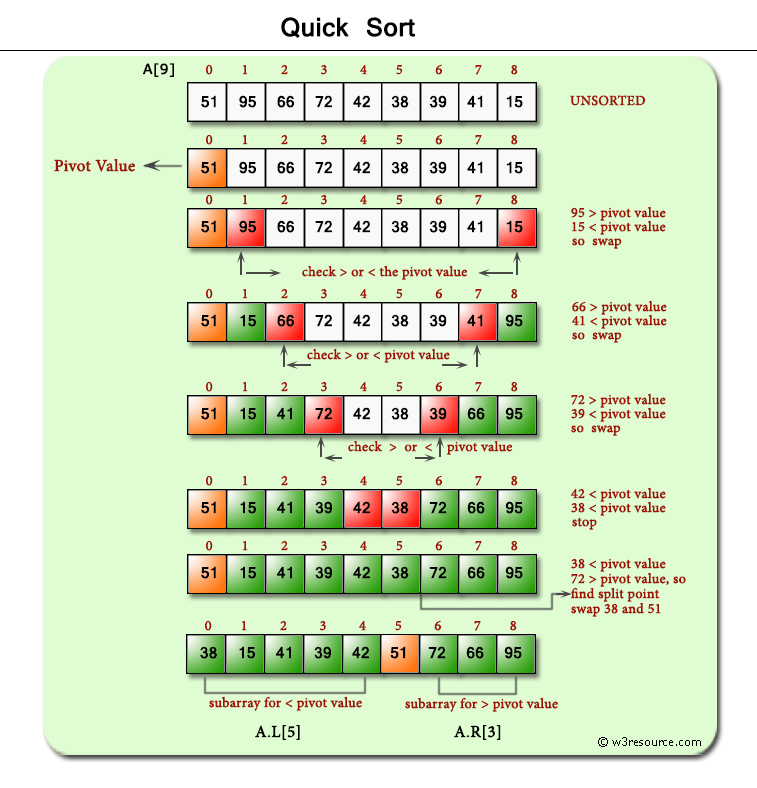
Quick Sort
Time Complexity: Quadratic O(n^2)
- Even though the average time complexity O(nLog(n)), the worst case scenario is always quadratic.
Space Complexity: O(n)
- Our space complexity is linear O(n) because of the partition arrays we create.
- QS is another Divide and Conquer strategy.
- Some key ideas to keep in mind:
- It is easy to sort elements of an array relative to a particular target value.
- An array of 0 or 1 elements is already trivially sorted.
function quickSort(array) {
if (array.length <= 1) return array;
let pivot = array.shift();
let left = array.filter((x) => x < pivot);
let right = array.filter((x) => x >= pivot);
let sortedLeft = quickSort(left);
let sortedRight = quickSort(right);
return [...sortedLeft, pivot, ...sortedRight];
} |
view rawquicksort.js hosted with ❤ by GitHub
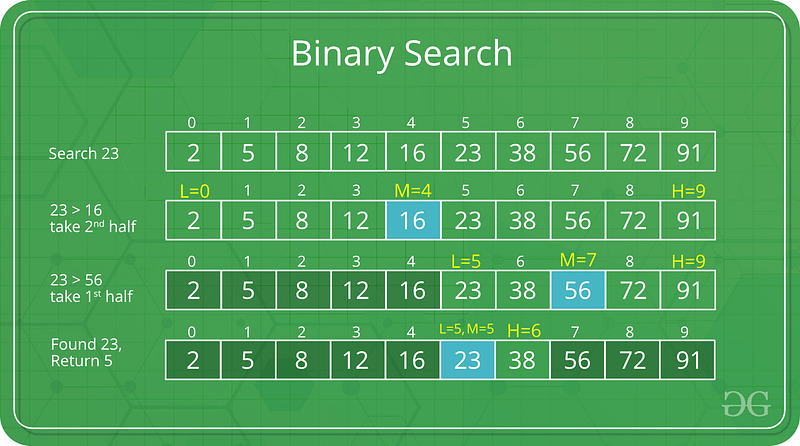
Binary Search
Time Complexity: Log Time O(log(n))
Space Complexity: O(1)
Recursive Solution
function binarySearch(array, target) {
if (array.length === 0) return false;
let midPt = Math.floor(array.length / 2);
if (array[midPt] === target) {
return true;
} else if (list[midPt] > target) {
return binarySearch(list.slice(0, mid), target);
} else {
return binarySearch(list.slice(midPt + 1), target);
}
} |
view rawrecur-bin-search.js hosted with ❤ by GitHub
Min Max Solution
function binarySearch(array, target) {
let start = 0;
let end = array.length - 1;
while (start <= end) {
let midpoint = Math.floor((start + end) / 2);
if (target === array[midpoint]) {
return midpoint;
}
if (target > array[midpoint]) {
start = midpoint + 1;
}
if (target < array[midpoint]) {
end = midpoint - 1;
}
}
return -1;
} |
view rawminmaxbinsearch.js hosted with ❤ by GitHub
function binarySearch(arr, x, start, end) {
if (start > end) return false;
let mid = Math.floor((start + end) / 2);
if (arr[mid] === x) return true;
if (arr[mid] > x) {
return binarySearch(arr, x, start, mid - 1);
} else {
return binarySearch(arr, x, mid + 1, end);
}
} |
view rawbinsearch.js hosted with ❤ by GitHub
- Must be conducted on a sorted array.
- Binary search is logarithmic time, not exponential b/c n is cut down by two, not growing.
- Binary Search is part of Divide and Conquer.
Insertion Sort
- Works by building a larger and larger sorted region at the left-most end of the array.
Steps:
- If it is the first element, and it is already sorted; return 1.
- Pick next element.
- Compare with all elements in the sorted sub list
- Shift all the elements in the sorted sub list that is greater than the value to be sorted.
- Insert the value
- Repeat until list is sorted.
let insertionSort = (inputArr) => {
let length = inputArr.length;
for (let i = 1; i < length; i++) {
let key = inputArr[i];
let j = i - 1;
while (j >= 0 && inputArr[j] > key) {
inputArr[j + 1] = inputArr[j];
j = j - 1;
}
inputArr[j + 1] = key;
}
return inputArr;
}; |
view rawinsertionsort.js hosted with ❤ by GitHub
If you found this guide helpful feel free to checkout my GitHub/gists where I host similar content:
bgoonz's gists
Instantly share code, notes, and snippets. Web Developer, Electrical Engineer JavaScript | CSS | Bootstrap | Python |...gist.github.com
bgoonz --- Overview
Web Developer, Electrical Engineer JavaScript | CSS | Bootstrap | Python | React | Node.js | Express | Sequelize...github.com
Or Checkout my personal Resource Site:
Web-Dev-Hub
Memoization, Tabulation, and Sorting Algorithms by Example Why is looking at runtime not a reliable method of...bgoonz-blog.netlify.app
/**************************************BIG-O***********************************/
/***********************Common Algorithms for Analysis********************/
//mdn Object;
//-**************-recursive factorial:*********************/
/*
Factorial: the product of a given positive integer multiplied by all lesser positive integers:
The quantity four factorial (4!) = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24.
Symbol:n!, where n is the given integer.
*/
function factorial(n) {
if (n === 1) return 1; //* Base Case ... 1 * 1 = 1
return n * factorial(n - 1); //* n! = n * (n-1) * (n-2) * (n-3) * ... * 1
}
factorial(5); //*5 * 4 * 3 * 2 * 1 = 120 <----expected
//console.log( "factorial(5): ", factorial( 5 ) ); //- factorial(5): 120
/*
Fibonacci numbers are the numbers such that every number in the series after the first two is the sum of the two preceding ones.
The series starts with 1, 1. Example -1, 1, 2, 3, 5, 8, 13, 21, 34, ....
Mathematical Expression: fib(n) = fib(n-1) + fib(n-2)
! fib-tree-structure-diagram.png
https://miro.medium.com/max/700/1*svQ784qk1hvBE3iz7VGGgQ.jpeg
*/
function fibonacci(n) {
if (n === 1 || n === 2) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
fibonacci(5);
//console.log("fib(5): ", fibonacci(5)); //- fib(5): 5
/*
the major differences between tabulation and memoization are:
1.) tabulation has to look through the entire search space; memoization does not
2.) tabulation requires careful ordering of the subproblems is; memoization doesn't care much about the order of recursive calls.
*/
const memo = {
0: 0,
1: 0,
2: 1
};
const fib = (n) => {
if (memo[n] !== undefined) return memo[n];
const n1 = fib(n - 1);
const n2 = fib(n - 2);
memo[n] = fib(n - 1) + fib(n - 2);
return memo[n];
};
//console.log("fib(50): ", fib(20)); //- fib(50): 4181
/******************End of Common Algorithms for Analysis*****************/
/***********Comparing two functions that calculate the sum of all numbers from 1 up to n**********************/
function addUpTo(n) {
let total = 0;
for (let i = 0; i <= n; i++) {
//! Number of operations will grow with input n.
total += i;
}
return total;
}
addUpTo(4);
//console.log("addUpTo( 4 ): ", addUpTo(4)); //- addUpTo( 4 ): 10
//! Would be O(n) or Linear Time.
//----------------------------------------------------------------
/*
The infinite series whose terms are the natural numbers 1 + 2 + 3 + 4 + ⋯ is a divergent series.
The nth partial sum of the series is the triangular number( https://en.wikipedia.org/wiki/Triangular_number )
addUpTo(n)=(n * (n + 1)) / 2
https://wikimedia.org/api/rest_v1/media/math/render/svg/99476e25466549387c585cb4de44e90f6cbe4cf2
*/
function constantAddUpTo(n) {
return (n * (n + 1)) / 2;
}
constantAddUpTo(4); //- constantAddUpTo(4): 10
//console.log("constantAddUpTo(4): ", constantAddUpTo(4));
//! Has three simple operations: 1 Multiplication 1 Addition 1 Division.
//!(Regardless of n) Would be O(1) or Constant Time.
/***********End of Comparing two functions that calculate the sum of all numbers from 1 up to n*******************/
/*
!Simplifying Math Terms
We want our Big-O notation to describe the performance of our algorithm with respect to the input size and nothing else.
!Use the following rules to simplify our Big-O functions using the following rules:
1.) Simplify Products: if the function is a product of many terms, we drop the terms that don't depend on the size of the input.
2.) Simplify Sums: if the function is a sum of many terms, we keep the term with the largest growth rate and drop the other terms.
* n is the size of the input
* T(f) refers to an un-simplified mathematical function
* O(f) refers to the Big-O simplified mathematical function
* Simplifying a Product
If a function consists of a product of many factors,
!we drop the factors that don't depend on the size of the input, n.
The factors that we drop are called constant factors because their size remains consistent as we increase the size of the input.
examples-of-big-O-simplification.png
simplifying-a-sum.png
simp-examples.png
*/
/***********Comparing two functions with nested for loops*********************/
// function countUpAndDown(n) {
// console.log("going up!");
// for (let i = 0; i < n; i++) {
// console.log(i);
// }
// console.log("at the top, going down!");
// for (let j = n - 1; j >= 0; j--) {
// console.log(j);
// }
// console.log("Back down, bye!");
// }
// countUpAndDown(5);
// console.log("countUpAndDown(5): ", countUpAndDown(5));
/*
going up!
0 1 2 3 4
at the top, going down!
4 3 2 1 0
Back down, bye!
countUpAndDown(5): undefined //- because there was no return statment... only console.log
*/
//------------------------------------------------
//!Both loops are O(n) but since we just want the big picture, O(n);
//-----------------------------------------------
// function printAllPairs(n) {
// for (let i = 0; i < n; i++) {
// for (let j = 0; j < n; j++) {
// console.log(i, j);
// }
// }
// }
// printAllPairs(4);
/*
0 0 0 1 0 2 0 3 1 0 1 1 1 2 1 3 2 0 2 1 2 2 2 3 3 0 3 1 3 2 3 3
*/
//!Nested loops who's number of iterations depend on the size of the input are never a good thing when trying to write fast code.
//!O(n^2) or Quadratic Time.
/***********END of Comparing two functions with nested for loops**********************/
/**************************Big-O-Operations**********************/
//! Arithmetic Operations are Constant
//! Variable assignment is constant
//! Accessing elements in an array (by index) or by object (by key) is constant.
//! In a loop, the complexity is the length of the loop times the complexity of whatever is inside of the loop.
/**************************More Examples**********************/
//---------------------logAtLeast5---------------------------------
function logAtLeast5(n) {
for (let i = 1; i <= Math.max(5, n); i++) {
//console.log(i);
}
}
//! O(n) Linear Time
//logAtLeast5(2);
/*
1 2 3 4 5
----------------------------
*/
//logAtLeast5(6);
/*
----------------------------
1 2 3 4 5 6
*/
//---------------------logAtMost5---------------------------------
function logAtMost5(n) {
for (var i = 1; i <= Math.min(5, n); i++) {
//console.log(i);
}
}
logAtMost5(20);
//! O(1) Constant Time.
/*
1 2 3 4 5
*/
//***********************Big-O Complexity Classes*************************** */
/*
//! O(1) Constant
The algorithm takes roughly the same number of steps for any input size.
*/
function constant1(n) {
return n * 2 + 1;
}
constant1(5); //constant1(5): 11
//console.log("constant1(5): ", constant1(5));
//--------
//! O(1)
//--------
function constant2(n) {
for (let i = 1; i <= 100; i++) {
console.log(i);
}
}
//constant2(5);
////console.log("constant2(5): ", constant2(5));
//1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
//------------------------------------------
/*
O(log(n)) Logarithmic
In most cases our hidden base of Logarithmic time is 2,
log complexity algo's will typically display 'halving' the size of the input ??
? (like binary search!)
*/
// O(log(n))
function logarithmic1(n) {
if (n <= 1) {
return 'base case';
} else {
return logarithmic1(n / 2); //*Recursive call on **half** the input
}
}
//! O(log(n))
function logarithmic2(n) {
let i = n;
while (i > 1) {
i /= 2;
return i;
}
}
logarithmic1(5);
////console.log("logarithmic1(5): ", logarithmic1(5)); //logarithmic1(5): base case
logarithmic2(6);
////console.log("logarithmic2(6): ", logarithmic2(6)); //logarithmic2(6): 3
//------------------------------------------
/*
* O(n) Linear
Linear algo's will access each item of the input "once".
*/
// O(n)
function linear1(n) {
for (let i = 1; i <= n; i++) {
//console.log("linear1", i);
}
}
linear1(3);
/*
linear1 1
linear1 2
linear1 3
*/
// O(n), where n is the length of the array
function linear2(array) {
for (let i = 0; i < array.length; i++) {
//console.log("linear2", i);
}
}
linear2([1, 2, 3]);
/*
linear2 0
linear2 1
linear2 2
*/
//! O(n)
function linear3(n) {
if (n === 1) {
return 1;
} else {
//console.log(`linear3(${n})--->`, linear3(n - 1));
/*
*/
}
}
//!linear3(6);
//linear3(2)---> 1 linear3(3)---> undefined linear3(4)---> undefined
//linear3(5)---> undefined linear3(6)---> undefined
//!linear3(5);
// linear3(2)---> 1 linear3(3)---> undefined linear3(4)---> undefined
//linear3(5)---> undefined
//// in the two function calls above we can see that size of output corresponds to a proportional change in the size of the input
//console.log("linear3(4): ", linear3(4)); //// linear3(4): undefined
//------------------------------------------
/*
* O(nlog(n)) Log Linear Time
Combination of linear and logarithmic behavior,
we will see features from both classes.
!Algorithm's that are log-linear will use both recursion AND iteration.
*/
// O(n * log(n))
// function loglinear(n) {
// if (n <= 1) return; // base case
// for (let i = 1; i <= n; i++) {
// console.log(
// `for an input (n=${n}):`,
// `we are on the ${i}'th itteration where i = ${i}`
// );
// }
// console.log(" first call n('old n'):", n);
// loglinear(n / 2);
// console.log(` new n is = (${n})`);
// }
// loglinear(4);
/*
for an input (n=4): we are on the 1'th itteration where i = 1
for an input (n=4): we are on the 2'th itteration where i = 2
for an input (n=4): we are on the 3'th itteration where i = 3
for an input (n=4): we are on the 4'th itteration where i = 4
first call n('old n'): 4
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2
new n is = (2)
new n is = (4)
*/
function loglinear(n) {
if (n <= 1) return; // base case
for (let i = 1; i <= n; i++) {
console.log(`for an input (n=${n}):`, `we are on the ${i}'th itteration where i = ${i}`);
}
console.log(" first call n('old n'):", n, `new n is = (${n / 2})`);
loglinear(n / 2);
console.log(` new n is = (${n})`);
loglinear(n / 2);
console.log(` Second Call : new n is = (${n})`);
}
//loglinear(4);
/*
for an input (n=4): we are on the 1'th itteration where i = 1
for an input (n=4): we are on the 2'th itteration where i = 2
for an input (n=4): we are on the 3'th itteration where i = 3
for an input (n=4): we are on the 4'th itteration where i = 4
first call n('old n'): 4 new n is = (2)
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2 new n is = (1)
new n is = (2)
Second Call : new n is = (2)
new n is = (4)
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2 new n is = (1)
new n is = (2)
Second Call : new n is = (2)
Second Call : new n is = (4)
*/
//------------------------------------------
/*
O(nc) Polynomial
C is a fixed constant.
*/
// O(n^3)
function cubic(n) {
let count = 0;
for (let i = 1; i <= n; i++) {
//console.log(`i is ${i}`, "count:", count);
for (let j = 1; j <= n; j++) {
//console.log(` for i: ${i} j is:${j}`);
for (let k = 1; k <= n; k++) {
count += 1;
// console.log( ` itteration #${count}: i: is ${i}, j: is ${j}, k:is ${k}`);
}
}
}
}
cubic(3);
/*
i is 1 count: 0
for i: 1 j is:1
itteration #1: i: is 1, j: is 1, k: is 1
itteration #2: i: is 1, j: is 1, k: is 2
itteration #3: i: is 1, j: is 1, k: is 3
for i: 1 j is:2
itteration #4: i: is 1, j: is 2, k: is 1
itteration #5: i: is 1, j: is 2, k: is 2
itteration #6: i: is 1, j: is 2, k: is 3
for i: 1 j is:3
itteration #7: i: is 1, j: is 3, k: is 1
itteration #8: i: is 1, j: is 3, k: is 2
itteration #9: i: is 1, j: is 3, k: is 3
i is 2 count: 9
for i: 2 j is:1
itteration #10: i: is 2, j: is 1, k: is 1
itteration #11: i: is 2, j: is 1, k: is 2
itteration #12: i: is 2, j: is 1, k: is 3
for i: 2 j is:2
itteration #13: i: is 2, j: is 2, k: is 1
itteration #14: i: is 2, j: is 2, k: is 2
itteration #15: i: is 2, j: is 2, k: is 3
for i: 2 j is:3
itteration #16: i: is 2, j: is 3, k: is 1
itteration #17: i: is 2, j: is 3, k: is 2
itteration #18: i: is 2, j: is 3, k: is 3
i is 3 count: 18
for i: 3 j is:1
itteration #19: i: is 3, j: is 1, k: is 1
itteration #20: i: is 3, j: is 1, k: is 2
itteration #21: i: is 3, j: is 1, k: is 3
for i: 3 j is:2
itteration #22: i: is 3, j: is 2, k: is 1
itteration #23: i: is 3, j: is 2, k: is 2
itteration #24: i: is 3, j: is 2, k: is 3
for i: 3 j is:3
itteration #25: i: is 3, j: is 3, k: is 1
itteration #26: i: is 3, j: is 3, k: is 2
itteration #27: i: is 3, j: is 3, k: is 3
*/
//------------------------------------------
/*
Example of Quadratic and Cubic runtime.
!O(c^n) Exponential
C is now the number of recursive calls made in each stack frame.
-Algo's with exponential time are VERY SLOW.
*/
// O(3^n)
function exponential3n(n) {
if (n === 0) return;
//console.log("1.) first call n('old n'):", n, `....new n is = (${n - 1})`);
exponential3n(n - 1);
// console.log("---------------------(__1__)---------------------------", "\n");
// console.log(
// "2.) after first call ('old n'):",
// n,
// `....new n is = (${n - 1})`
// );
exponential3n(n - 1);
//console.log("-------------------------(__2__)---------------------", "\n");
//console.log(
// "3.) after second call ('old n'):",
// n,
// `....new n is = (${n - 1})`
// );
exponential3n(n - 1);
//console.log("-----------------------(__3__)-------------------------", "\n");
//console.log(
// "4.) after third call ('old n'):",
// n,
// `....new n is = (${n - 1})`
//);
}
exponential3n(3);
//***********************__Memoization__*************************** */
/*
Memoization : a design pattern used to reduce the overall number of calculations that can occur
in algorithms that use recursive strategies to solve.
MZ stores the results of the sub-problems in some other data structure, so that we can avoid
duplicate calculations and only 'solve' each problem once.
Two features that comprise memoization:
1\. FUNCTION MUST BE RECURSIVE.
2\. Our additional DS is usually an object (we refer to it as our memo!)
*/
//! _____Memoizing Factorial_____
// function fib(n, memo = {}) {
// if (n in memo) return memo[n]; // If we already calculated this value, return it
// if (n === 1 || n === 2) return 1;
// // Store the result in the memo first before returning
// // Make sure to pass the memo in to your calls to fib!
// memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
// return memo[n];
// }
function factorial(n, memo2 = {}) {
const key = JSON.stringify(n);
if (key in memo2) return memo2[key];
if (n === 1) return 1;
memo2[key] = n * factorial(n - 1, memo2);
//console.log("this is memo", memo2);
return memo2[key];
}
//console.log(memo2);
// //factorial(6); // => 720, requires 6 calls
//console.log("factorial(6): ", factorial(6));
// //factorial(6); // => 720, requires 1 call
// //factorial(5); // => 120, requires 1 call
// console.log("factorial(5): ", factorial(5));
//factorial(7); // => 5040, requires 2 calls
//console.log("factorial(7): ", factorial(7));
//console.log("factorial(20): ", factorial(20)); // 2432902008176640000
/*
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720 }
factorial(6): 720
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720, '7': 5040 }
factorial(7): 5040
*/
/*
The Memoization Formula
Rules
1\. Write the unoptimized brute force recursion (make sure it works);
2\. Add memo object as an additional arugmnt .
3\. Add a base case condition that returns the stored value if the function's argument is in the memo.
4\. Before returning the result of the recursive case, store it in the memo as a value and make the
function's argument it's key.
!Things to remember
*1. When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
*2. When you notice duplicate sub-tree's that means we can memoize.
*/
function fastFib(n, memo = {}) {
if (n in memo) return memo[n];
if (n === 1 || n === 2) return 1;
memo[n] = fastFib(n - 1, memo) + fastFib(n - 2, memo);
return memo[n];
}
//fastFib(6); // => 8
//console.log("fastFib(6): ", fastFib(6)); //fastFib(6): 8
//fastFib(50); // => 12586269025
//console.log("fastFib(50): ", fastFib(50)); //fastFib(50): 12586269025
//***********************__Tabulation__*************************** */
/*
Tabulation Strategy
//Use When:
-The function is iterative and not recursive.
-The accompanying Data Structure is usually an array.
*/
function fibTab(n) {
let table = [0, 1, 1];
// if(n === 0 || n === 1){
// return 1;
// }
while (table.length - 1 < n) {
table.push(table[table.length - 1] + table[table.length - 2]);
}
return table[n];
}
console.log(fibTab(1)); //1
console.log(fibTab(2)); //1
console.log(fibTab(3)); //2
console.log(fibTab(4)); //3
console.log(fibTab(5)); //5
console.log(fibTab(50)); //12586269025 |
view rawalgo-time-complexity-by-example.js hosted with ❤ by GitHub
Big O Examples In JavaScript
/**************************************BIG-O***********************************/
/***********************Common Algorithms for Analysis********************/
//mdn Object;
//-**************-recursive factorial:*********************/
/*
Factorial: the product of a given positive integer multiplied by all lesser positive integers:
The quantity four factorial (4!) = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24.
Symbol:n!, where n is the given integer.
*/
function factorial(n) {
if (n === 1) return 1; //* Base Case ... 1 * 1 = 1
return n * factorial(n - 1); //* n! = n * (n-1) * (n-2) * (n-3) * ... * 1
}
factorial(5); //*5 * 4 * 3 * 2 * 1 = 120 <----expected
//console.log( "factorial(5): ", factorial( 5 ) ); //- factorial(5): 120
/*
Fibonacci numbers are the numbers such that every number in the series after the first two is the sum of the two preceding ones.
The series starts with 1, 1. Example −1, 1, 2, 3, 5, 8, 13, 21, 34, ….
Mathematical Expression: fib(n) = fib(n−1) + fib(n−2)
! fib-tree-structure-diagram.png
https://miro.medium.com/max/700/1*svQ784qk1hvBE3iz7VGGgQ.jpeg
*/
function fibonacci(n) {
if (n === 1 || n === 2) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
fibonacci(5);
//console.log("fib(5): ", fibonacci(5)); //- fib(5): 5
/*
the major differences between tabulation and memoization are:
1.) tabulation has to look through the entire search space; memoization does not
2.) tabulation requires careful ordering of the subproblems is; memoization doesn't care much about the order of recursive calls.
*/
const memo = {
0: 0,
1: 0,
2: 1
};
const fib = (n) => {
if (memo[n] !== undefined) return memo[n];
const n1 = fib(n - 1);
const n2 = fib(n - 2);
memo[n] = fib(n - 1) + fib(n - 2);
return memo[n];
};
//console.log("fib(50): ", fib(20)); //- fib(50): 4181
/******************End of Common Algorithms for Analysis*****************/
/***********Comparing two functions that calculate the sum of all numbers from 1 up to n**********************/
function addUpTo(n) {
let total = 0;
for (let i = 0; i <= n; i++) {
//! Number of operations will grow with input n.
total += i;
}
return total;
}
addUpTo(4);
//console.log("addUpTo( 4 ): ", addUpTo(4)); //- addUpTo( 4 ): 10
//! Would be O(n) or Linear Time.
//----------------------------------------------------------------
/*
The infinite series whose terms are the natural numbers 1 + 2 + 3 + 4 + ⋯ is a divergent series.
The nth partial sum of the series is the triangular number( https://en.wikipedia.org/wiki/Triangular_number )
addUpTo(n)=(n * (n + 1)) / 2
https://wikimedia.org/api/rest_v1/media/math/render/svg/99476e25466549387c585cb4de44e90f6cbe4cf2
*/
function constantAddUpTo(n) {
return (n * (n + 1)) / 2;
}
constantAddUpTo(4); //- constantAddUpTo(4): 10
//console.log("constantAddUpTo(4): ", constantAddUpTo(4));
//! Has three simple operations: 1 Multiplication 1 Addition 1 Division.
//!(Regardless of n) Would be O(1) or Constant Time.
/***********End of Comparing two functions that calculate the sum of all numbers from 1 up to n*******************/
/*
!Simplifying Math Terms
We want our Big-O notation to describe the performance of our algorithm with respect to the input size and nothing else.
!Use the following rules to simplify our Big-O functions using the following rules:
1.) Simplify Products: if the function is a product of many terms, we drop the terms that don't depend on the size of the input.
2.) Simplify Sums: if the function is a sum of many terms, we keep the term with the largest growth rate and drop the other terms.
* n is the size of the input
* T(f) refers to an un-simplified mathematical function
* O(f) refers to the Big-O simplified mathematical function
* Simplifying a Product
If a function consists of a product of many factors,
!we drop the factors that don't depend on the size of the input, n.
The factors that we drop are called constant factors because their size remains consistent as we increase the size of the input.
examples-of-big-O-simplification.png
simplifying-a-sum.png
simp-examples.png
*/
/***********Comparing two functions with nested for loops*********************/
// function countUpAndDown(n) {
// console.log("going up!");
// for (let i = 0; i < n; i++) {
// console.log(i);
// }
// console.log("at the top, going down!");
// for (let j = n - 1; j >= 0; j--) {
// console.log(j);
// }
// console.log("Back down, bye!");
// }
// countUpAndDown(5);
// console.log("countUpAndDown(5): ", countUpAndDown(5));
/*
going up!
0 1 2 3 4
at the top, going down!
4 3 2 1 0
Back down, bye!
countUpAndDown(5): undefined //- because there was no return statment... only console.log
*/
//------------------------------------------------
//!Both loops are O(n) but since we just want the big picture, O(n);
//-----------------------------------------------
// function printAllPairs(n) {
// for (let i = 0; i < n; i++) {
// for (let j = 0; j < n; j++) {
// console.log(i, j);
// }
// }
// }
// printAllPairs(4);
/*
0 0 0 1 0 2 0 3 1 0 1 1 1 2 1 3 2 0 2 1 2 2 2 3 3 0 3 1 3 2 3 3
*/
//!Nested loops who's number of iterations depend on the size of the input are never a good thing when trying to write fast code.
//!O(n^2) or Quadratic Time.
/***********END of Comparing two functions with nested for loops**********************/
/**************************Big-O-Operations**********************/
//! Arithmetic Operations are Constant
//! Variable assignment is constant
//! Accessing elements in an array (by index) or by object (by key) is constant.
//! In a loop, the complexity is the length of the loop times the complexity of whatever is inside of the loop.
/**************************More Examples**********************/
//---------------------logAtLeast5---------------------------------
function logAtLeast5(n) {
for (let i = 1; i <= Math.max(5, n); i++) {
//console.log(i);
}
}
//! O(n) Linear Time
//logAtLeast5(2);
/*
1 2 3 4 5
----------------------------
*/
//logAtLeast5(6);
/*
----------------------------
1 2 3 4 5 6
*/
//---------------------logAtMost5---------------------------------
function logAtMost5(n) {
for (var i = 1; i <= Math.min(5, n); i++) {
//console.log(i);
}
}
logAtMost5(20);
//! O(1) Constant Time.
/*
1 2 3 4 5
*/
//***********************Big-O Complexity Classes*************************** */
/*
//! O(1) Constant
The algorithm takes roughly the same number of steps for any input size.
*/
function constant1(n) {
return n * 2 + 1;
}
constant1(5); //constant1(5): 11
//console.log("constant1(5): ", constant1(5));
//--------
//! O(1)
//--------
function constant2(n) {
for (let i = 1; i <= 100; i++) {
console.log(i);
}
}
//constant2(5);
////console.log("constant2(5): ", constant2(5));
//1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
//------------------------------------------
/*
O(log(n)) Logarithmic
In most cases our hidden base of Logarithmic time is 2,
log complexity algo's will typically display 'halving' the size of the input ??
? (like binary search!)
*/
// O(log(n))
function logarithmic1(n) {
if (n <= 1) {
return 'base case';
} else {
return logarithmic1(n / 2); //*Recursive call on **half** the input
}
}
//! O(log(n))
function logarithmic2(n) {
let i = n;
while (i > 1) {
i /= 2;
return i;
}
}
logarithmic1(5);
////console.log("logarithmic1(5): ", logarithmic1(5)); //logarithmic1(5): base case
logarithmic2(6);
////console.log("logarithmic2(6): ", logarithmic2(6)); //logarithmic2(6): 3
//------------------------------------------
/*
* O(n) Linear
Linear algo's will access each item of the input "once".
*/
// O(n)
function linear1(n) {
for (let i = 1; i <= n; i++) {
//console.log("linear1", i);
}
}
linear1(3);
/*
linear1 1
linear1 2
linear1 3
*/
// O(n), where n is the length of the array
function linear2(array) {
for (let i = 0; i < array.length; i++) {
//console.log("linear2", i);
}
}
linear2([1, 2, 3]);
/*
linear2 0
linear2 1
linear2 2
*/
//! O(n)
function linear3(n) {
if (n === 1) {
return 1;
} else {
//console.log(`linear3(${n})--->`, linear3(n - 1));
/*
*/
}
}
//!linear3(6);
//linear3(2)---> 1 linear3(3)---> undefined linear3(4)---> undefined
//linear3(5)---> undefined linear3(6)---> undefined
//!linear3(5);
// linear3(2)---> 1 linear3(3)---> undefined linear3(4)---> undefined
//linear3(5)---> undefined
//// in the two function calls above we can see that size of output corresponds to a proportional change in the size of the input
//console.log("linear3(4): ", linear3(4)); //// linear3(4): undefined
//------------------------------------------
/*
* O(nlog(n)) Log Linear Time
Combination of linear and logarithmic behavior,
we will see features from both classes.
!Algorithm's that are log-linear will use both recursion AND iteration.
*/
// O(n * log(n))
// function loglinear(n) {
// if (n <= 1) return; // base case
// for (let i = 1; i <= n; i++) {
// console.log(
// `for an input (n=${n}):`,
// `we are on the ${i}'th itteration where i = ${i}`
// );
// }
// console.log(" first call n('old n'):", n);
// loglinear(n / 2);
// console.log(` new n is = (${n})`);
// }
// loglinear(4);
/*
for an input (n=4): we are on the 1'th itteration where i = 1
for an input (n=4): we are on the 2'th itteration where i = 2
for an input (n=4): we are on the 3'th itteration where i = 3
for an input (n=4): we are on the 4'th itteration where i = 4
first call n('old n'): 4
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2
new n is = (2)
new n is = (4)
*/
function loglinear(n) {
if (n <= 1) return; // base case
for (let i = 1; i <= n; i++) {
console.log(`for an input (n=${n}):`, `we are on the ${i}'th itteration where i = ${i}`);
}
console.log(" first call n('old n'):", n, `new n is = (${n / 2})`);
loglinear(n / 2);
console.log(` new n is = (${n})`);
loglinear(n / 2);
console.log(` Second Call : new n is = (${n})`);
}
//loglinear(4);
/*
for an input (n=4): we are on the 1'th itteration where i = 1
for an input (n=4): we are on the 2'th itteration where i = 2
for an input (n=4): we are on the 3'th itteration where i = 3
for an input (n=4): we are on the 4'th itteration where i = 4
first call n('old n'): 4 new n is = (2)
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2 new n is = (1)
new n is = (2)
Second Call : new n is = (2)
new n is = (4)
for an input (n=2): we are on the 1'th itteration where i = 1
for an input (n=2): we are on the 2'th itteration where i = 2
first call n('old n'): 2 new n is = (1)
new n is = (2)
Second Call : new n is = (2)
Second Call : new n is = (4)
*/
//------------------------------------------
/*
O(nc) Polynomial
C is a fixed constant.
*/
// O(n^3)
function cubic(n) {
let count = 0;
for (let i = 1; i <= n; i++) {
//console.log(`i is ${i}`, "count:", count);
for (let j = 1; j <= n; j++) {
//console.log(` for i: ${i} j is:${j}`);
for (let k = 1; k <= n; k++) {
count += 1;
// console.log( ` itteration #${count}: i: is ${i}, j: is ${j}, k:is ${k}`);
}
}
}
}
cubic(3);
/*
i is 1 count: 0
for i: 1 j is:1
itteration #1: i: is 1, j: is 1, k: is 1
itteration #2: i: is 1, j: is 1, k: is 2
itteration #3: i: is 1, j: is 1, k: is 3
for i: 1 j is:2
itteration #4: i: is 1, j: is 2, k: is 1
itteration #5: i: is 1, j: is 2, k: is 2
itteration #6: i: is 1, j: is 2, k: is 3
for i: 1 j is:3
itteration #7: i: is 1, j: is 3, k: is 1
itteration #8: i: is 1, j: is 3, k: is 2
itteration #9: i: is 1, j: is 3, k: is 3
i is 2 count: 9
for i: 2 j is:1
itteration #10: i: is 2, j: is 1, k: is 1
itteration #11: i: is 2, j: is 1, k: is 2
itteration #12: i: is 2, j: is 1, k: is 3
for i: 2 j is:2
itteration #13: i: is 2, j: is 2, k: is 1
itteration #14: i: is 2, j: is 2, k: is 2
itteration #15: i: is 2, j: is 2, k: is 3
for i: 2 j is:3
itteration #16: i: is 2, j: is 3, k: is 1
itteration #17: i: is 2, j: is 3, k: is 2
itteration #18: i: is 2, j: is 3, k: is 3
i is 3 count: 18
for i: 3 j is:1
itteration #19: i: is 3, j: is 1, k: is 1
itteration #20: i: is 3, j: is 1, k: is 2
itteration #21: i: is 3, j: is 1, k: is 3
for i: 3 j is:2
itteration #22: i: is 3, j: is 2, k: is 1
itteration #23: i: is 3, j: is 2, k: is 2
itteration #24: i: is 3, j: is 2, k: is 3
for i: 3 j is:3
itteration #25: i: is 3, j: is 3, k: is 1
itteration #26: i: is 3, j: is 3, k: is 2
itteration #27: i: is 3, j: is 3, k: is 3
*/
//------------------------------------------
/*
Example of Quadratic and Cubic runtime.
!O(c^n) Exponential
C is now the number of recursive calls made in each stack frame.
-Algo's with exponential time are VERY SLOW.
*/
// O(3^n)
function exponential3n(n) {
if (n === 0) return;
//console.log("1.) first call n('old n'):", n, `....new n is = (${n - 1})`);
exponential3n(n - 1);
// console.log("---------------------(__1__)---------------------------", "\n");
// console.log(
// "2.) after first call ('old n'):",
// n,
// `....new n is = (${n - 1})`
// );
exponential3n(n - 1);
//console.log("-------------------------(__2__)---------------------", "\n");
//console.log(
// "3.) after second call ('old n'):",
// n,
// `....new n is = (${n - 1})`
// );
exponential3n(n - 1);
//console.log("-----------------------(__3__)-------------------------", "\n");
//console.log(
// "4.) after third call ('old n'):",
// n,
// `....new n is = (${n - 1})`
//);
}
exponential3n(3);
//***********************__Memoization__*************************** */
/*
Memoization : a design pattern used to reduce the overall number of calculations that can occur
in algorithms that use recursive strategies to solve.
MZ stores the results of the sub-problems in some other data structure, so that we can avoid
duplicate calculations and only 'solve' each problem once.
Two features that comprise memoization:
1. FUNCTION MUST BE RECURSIVE.
2. Our additional DS is usually an object (we refer to it as our memo!)
*/
//! _____Memoizing Factorial_____
// function fib(n, memo = {}) {
// if (n in memo) return memo[n]; // If we already calculated this value, return it
// if (n === 1 || n === 2) return 1;
// // Store the result in the memo first before returning
// // Make sure to pass the memo in to your calls to fib!
// memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
// return memo[n];
// }
function factorial(n, memo2 = {}) {
const key = JSON.stringify(n);
if (key in memo2) return memo2[key];
if (n === 1) return 1;
memo2[key] = n * factorial(n - 1, memo2);
//console.log("this is memo", memo2);
return memo2[key];
}
//console.log(memo2);
// //factorial(6); // => 720, requires 6 calls
//console.log("factorial(6): ", factorial(6));
// //factorial(6); // => 720, requires 1 call
// //factorial(5); // => 120, requires 1 call
// console.log("factorial(5): ", factorial(5));
//factorial(7); // => 5040, requires 2 calls
//console.log("factorial(7): ", factorial(7));
//console.log("factorial(20): ", factorial(20)); // 2432902008176640000
/*
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720 }
factorial(6): 720
this is memo { '2': 2 }
this is memo { '2': 2, '3': 6 }
this is memo { '2': 2, '3': 6, '4': 24 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720 }
this is memo { '2': 2, '3': 6, '4': 24, '5': 120, '6': 720, '7': 5040 }
factorial(7): 5040
*/
/*
The Memoization Formula
Rules
1. Write the unoptimized brute force recursion (make sure it works);
2. Add memo object as an additional arugmnt .
3. Add a base case condition that returns the stored value if the function's argument is in the memo.
4. Before returning the result of the recursive case, store it in the memo as a value and make the
function's argument it's key.
!Things to remember
*1. When solving DP problems with Memoization, it is helpful to draw out the visual tree first.
*2. When you notice duplicate sub-tree's that means we can memoize.
*/
function fastFib(n, memo = {}) {
if (n in memo) return memo[n];
if (n === 1 || n === 2) return 1;
memo[n] = fastFib(n - 1, memo) + fastFib(n - 2, memo);
return memo[n];
}
//fastFib(6); // => 8
//console.log("fastFib(6): ", fastFib(6)); //fastFib(6): 8
//fastFib(50); // => 12586269025
//console.log("fastFib(50): ", fastFib(50)); //fastFib(50): 12586269025
//***********************__Tabulation__*************************** */
/*
Tabulation Strategy
//Use When:
-The function is iterative and not recursive.
-The accompanying Data Structure is usually an array.
*/
function fibTab(n) {
let table = [0, 1, 1];
// if(n === 0 || n === 1){
// return 1;
// }
while (table.length - 1 < n) {
table.push(table[table.length - 1] + table[table.length - 2]);
}
return table[n];
}
console.log(fibTab(1)); //1
console.log(fibTab(2)); //1
console.log(fibTab(3)); //2
console.log(fibTab(4)); //3
console.log(fibTab(5)); //5
console.log(fibTab(50)); //12586269025