What are data structures
Data structures, at a high level, are techniques for storing and organizing data that make it easier to modify, navigate, and access. Data structures determine how data is collected, the functions we can use to access it, and the relationships between data.
Data structures are used in almost all areas of computer science and programming, from operating systems to basic vanilla code to artificial intelligence.
Data structures enable us to:
- Manage and utilize large datasets
- Search for particular data from a database
- Design algorithms that are tailored towards particular programs
- Handle multiple requests from users at once
- Simplify and speed up data processing
Data structures are vital for efficient, real-world problem solving. After all, the way we organize data has a lot of impact on performance and useability. In fact, most top companies require a strong understanding of data structures.
Anyone looking to crack the coding interview will need to master data structures.
JavaScript has primitive and non-primitive data structures. Primitive data structures and data types are native to the programming language. These include boolean, null, number, string, etc.
Non-primitive data structures are not defined by the programming language but rather by the programmer. These include linear data structures, static data structures, and dynamic data structures, like queue and linked lists.
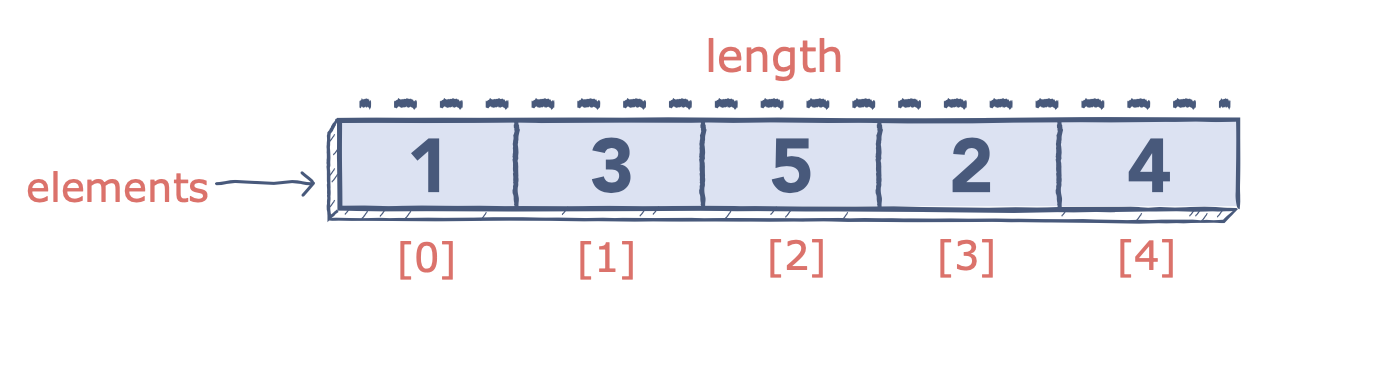
1. Array
The most basic of all data structures, an array stores data in memory for later use. Each array has a fixed number of cells decided on its creation, and each cell has a corresponding numeric index used to select its data. Whenever you'd like to use the array, all you need are the desired indices, and you can access any of the data within.
Advantages
- Simple to create and use.
- Foundational building block for complex data structures
Disadvantages
- Fixed size
- Expensive to insert/delete or resequence values
- Inefficient to sort
Applications
- Basic spreadsheets
- Within complex structures such as hash tables
2. Queues
Queues are conceptually similar to stacks; both are sequential structures, but queues process elements in the order they were entered rather than the most recent element.
As a result, queues can be thought of as a FIFO (First In, First Out) version of stacks. These are helpful as a buffer for requests, storing each request in the order it was received until it can be processed.
For a visual, consider a single-lane tunnel: the first car to enter is the first car to exit. If other cars should wish to exit, but the first stops, all cars will have to wait for the first to exit before they can proceed.
Advantages
- Dynamic size
- Orders data in the order it was received
- Low runtime
Disadvantages
- Can only retrieve the oldest element
Applications
- Effective as a buffer when receiving frequent data
- Convenient way to store order-sensitive data such as stored voicemails
- Ensures the oldest data is processed first
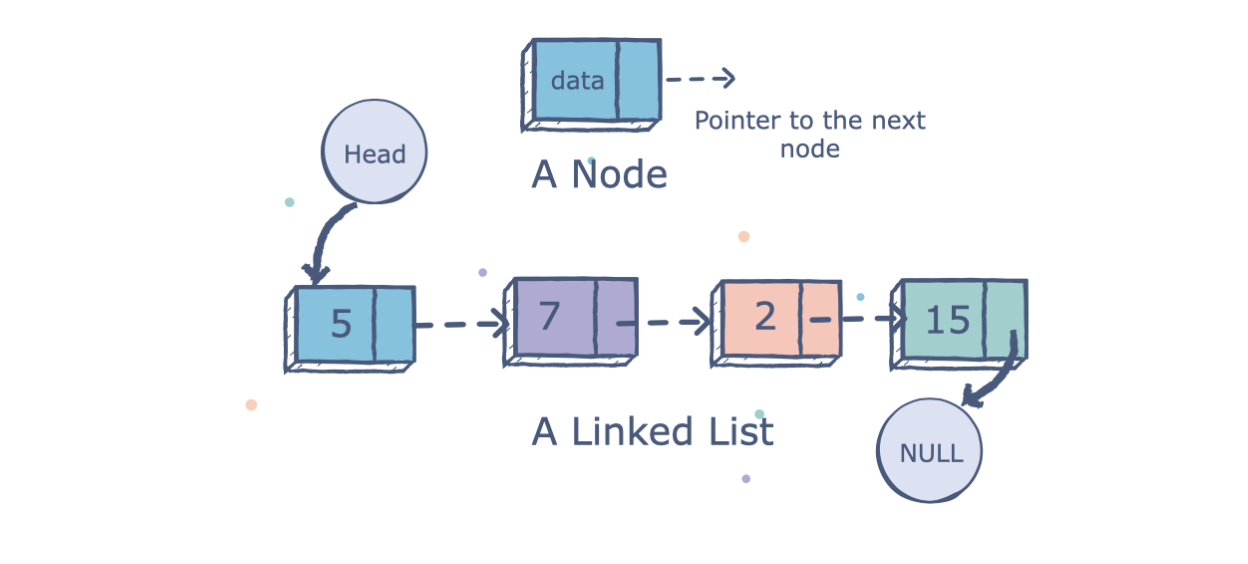
3. Linked List
Linked lists are a data structure which, unlike the previous three, does not use physical placement of data in memory. This means that, rather than indexes or positions, linked lists use a referencing system: elements are stored in nodes that contain a pointer to the next node, repeating until all nodes are linked.
This system allows efficient insertion and removal of items without the need for reorganization.
Advantages
- Efficient insertion and removal of new elements
- Less complex than restructuring an array
Disadvantages
- Uses more memory than arrays
- Inefficient to retrieve a specific element
- Inefficient to traverse the list backward
Applications
- Best used when data must be added and removed in quick succession from unknown locations
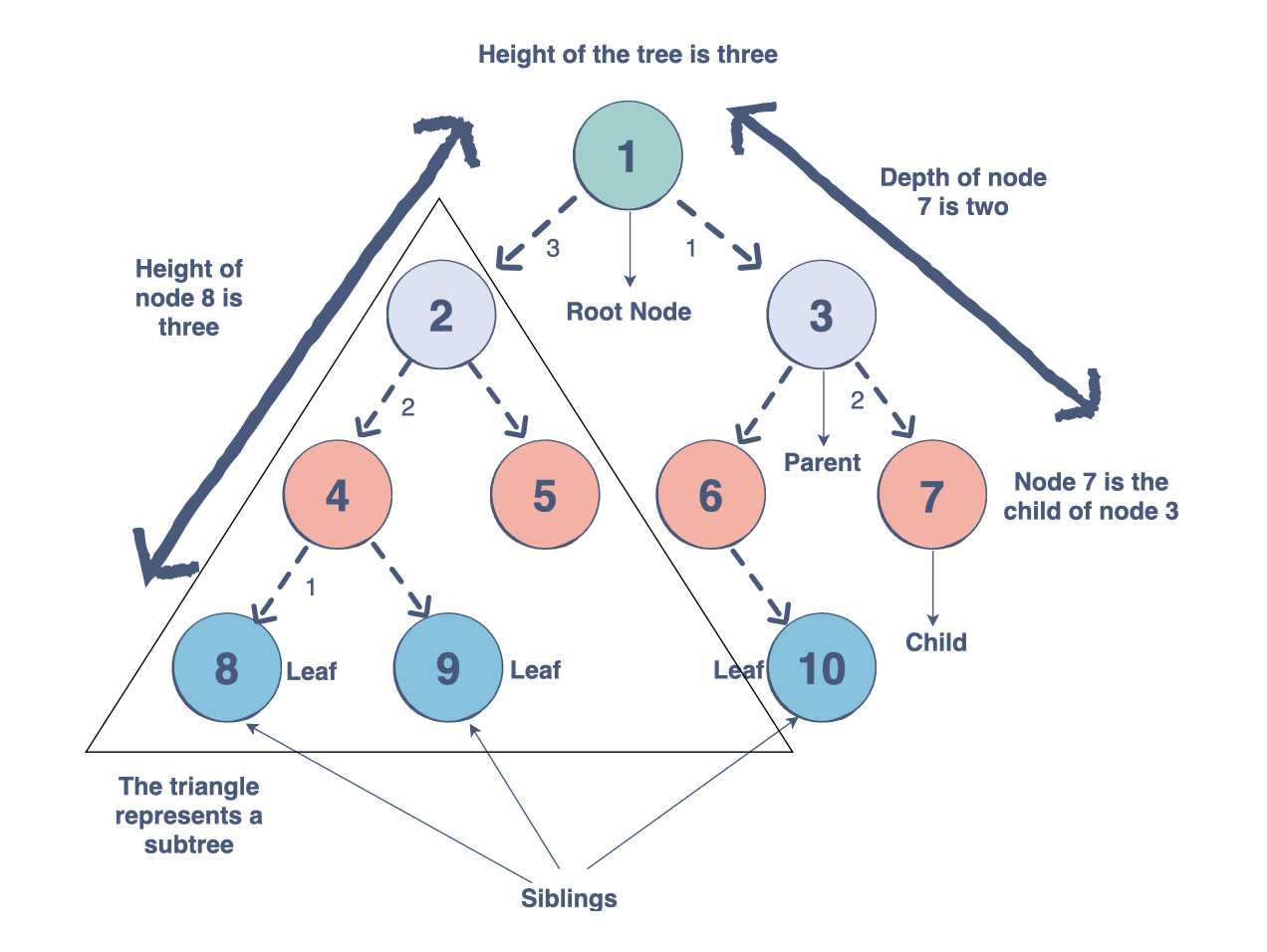
4. Trees
Trees are another relation-based data structure, which specialize in representing hierarchical structures. Like a linked list, nodes contain both elements of data and pointers marking its relation to immediate nodes.
Each tree has a "root" node, off of which all other nodes branch. The root contains references to all elements directly below it, which are known as its "child nodes". This continues, with each child node, branching off into more child nodes.
Nodes with linked child nodes are called internal nodes while those without child nodes are external nodes. A common type of tree is the "binary search tree" which is used to easily search stored data.
These search operations are highly efficient, as its search duration is dependent not on the number of nodes but on the number of levels down the tree.
This type of tree is defined by four strict rules:
- The left subtree contains only nodes with elements lesser than the root.
- The right subtree contains only nodes with elements greater than the root.
- Left and right subtrees must also be a binary search tree. They must follow the above rules with the "root" of their tree.
- There can be no duplicate nodes, i.e. no two nodes can have the same value.
Advantages
- Ideal for storing hierarchical relationships
- Dynamic size
- Quick at insert and delete operations
- In a binary search tree, inserted nodes are sequenced immediately.
- Binary search trees are efficient at searches; length is only O(height)O(height).
Disadvantages
- Slow to rearrange nodes
- Child nodes hold no information about their parent node
- Binary search trees are not as fast as the more complicated hash table
- Binary search trees can degenerate into linear search (scanning all elements) if not implemented with balanced subtrees.
Applications
- Storing hierarchical data such as a file location.
- Binary search trees are excellent for tasks needing searching or ordering of data.
Enjoying the article? Scroll down to sign up for our free, bi-monthly newsletter.
5. Graphs
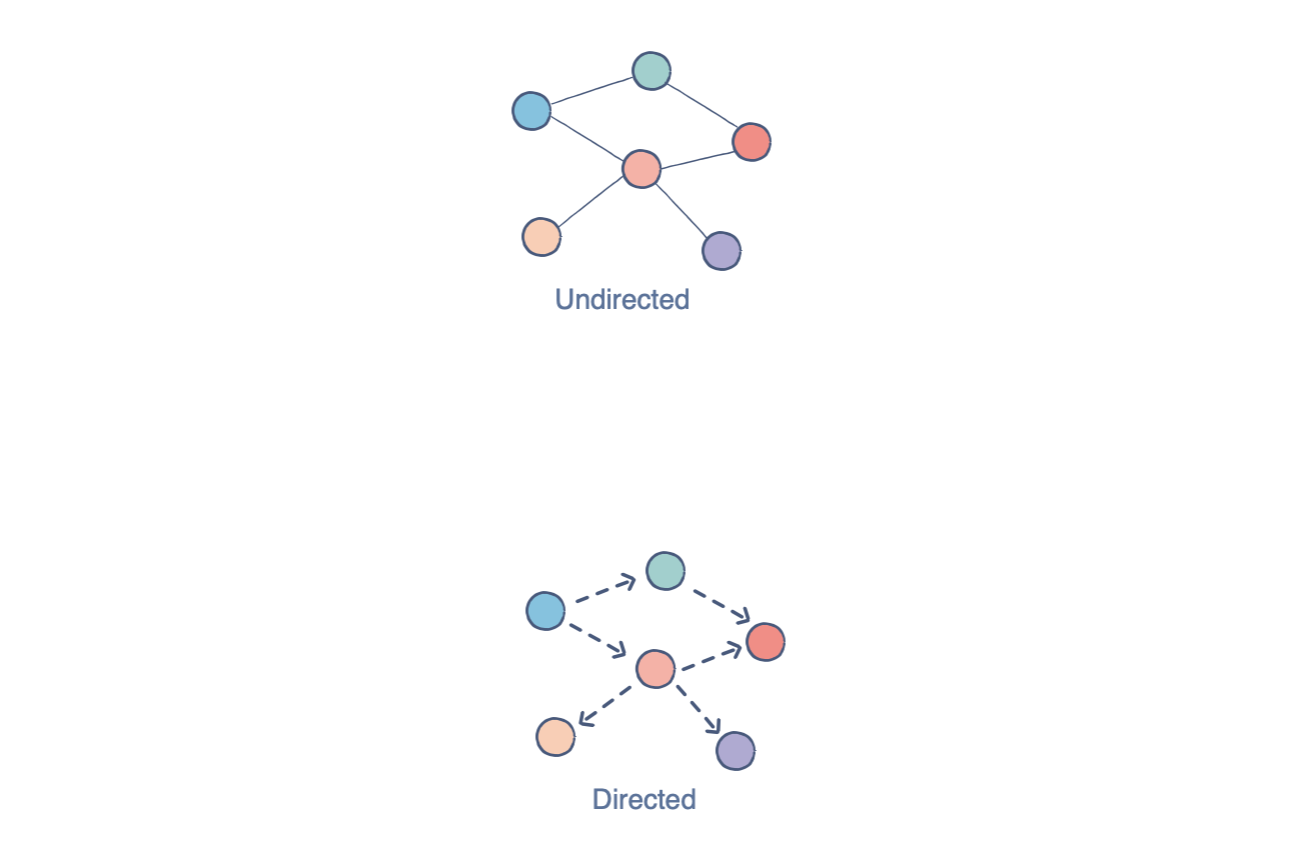
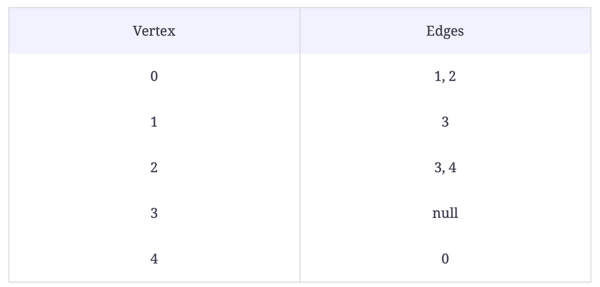
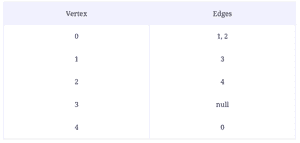
Graphs are a relation-based data structure helpful for storing web-like relationships. Each node, or vertex, as they're called in graphs, has a title (A, B, C, etc.), a value contained within, and a list of links (called edges) it has with other vertices.
In the above example, each circle is a vertex, and each line is an edge. If produced in writing, this structure would look like:
V = {a, b, c, d}
E = {ab, ac, bc, cd}
While hard to visualize at first, this structure is invaluable in conveying relationship charts in textual form, anything from circuitry to train networks.
Advantages
- Can quickly convey visuals over text
- Usable to model a diverse number of subjects so long as they contain a relational structure
Disadvantages
- At a higher level, text can be time-consuming to convert to an image.
- It can be difficult to see the existing edges or how many edges a given vertex has connected to it
Applications
- Network representations
- Modeling social networks, such as Facebook.
6. Hash Tables (Map)
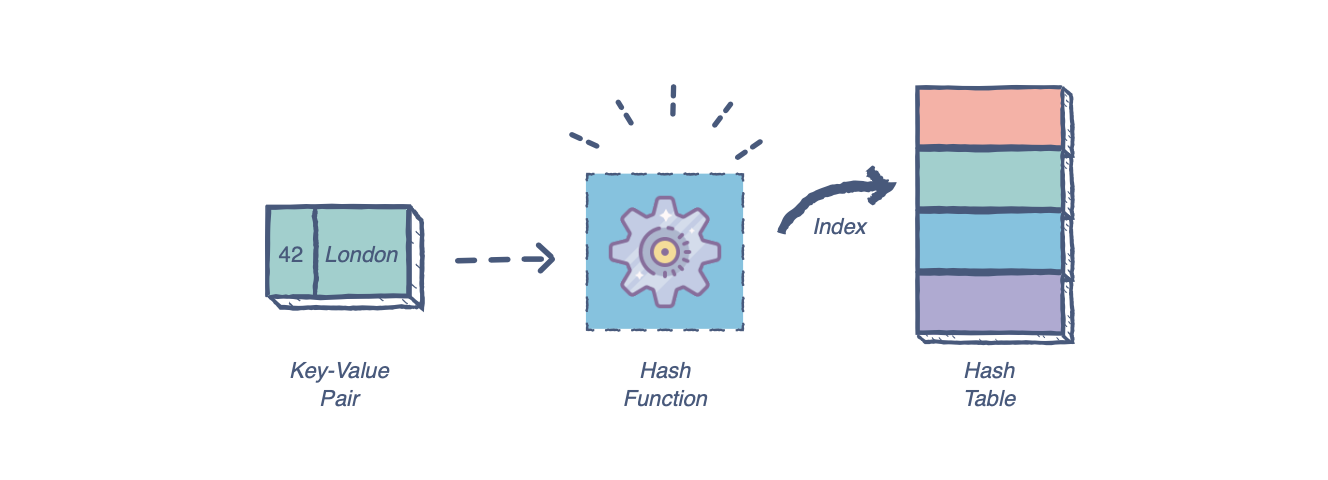
Hash tables are a complex data structure capable of storing large amounts of information and retrieving specific elements efficiently. This data structure relies on the concept of key/value pairs, where the "key" is a searched string and the "value" is the data paired with that key.
Advantages
- Key can be in any form, while array's indices must be integers
- Highly efficient search function
- Constant number of operations for each search
- Constant cost for insertion or deletion operations
Disadvantages
- Collisions: an error caused when two keys convert to the same hash code or two hash codes point to the same value.
- These errors can be common and often require an overhaul of the hash function.
Applications
- Database storage
- Address lookups by name
Each hash table can be very different, from the types of the keys and values, to the way their hash functions work. Due to these differences and the multi-layered aspects of a hash table, it is nearly impossible to encapsulate so generally.
Data structure interview questions
🔥See Interview Questions
For many developers and programmers, data structures are most important for cracking Javascript coding interviews. Questions and problems on data structures are fundamental to modern-day coding interviews. In fact, they have a lot to say over your hireability and entry-level rate as a candidate.
Today, we will be going over seven common coding interview questions for JavaScript data structures, one for each of the data structures we discussed above. Each will also discuss its time complexity based on the BigO notation theory.
Array: Remove all even integers from an array
Problem statement: Implement a function removeEven(arr), which takes an array arr in its input and removes all the even elements from a given array.
Input: An array of random integers
[1,2,4,5,10,6,3]
Output: an array containing only odd integers
[1,5,3]
There are two ways you could solve this coding problem in an interview. Let's discuss each.
Solution #1: Doing it "by hand"
function removeEven(arr) {
const odds = [];
for (let number of arr) {
if (number % 2 != 0)
// Check if the item in the list is NOT even ('%' is the modulus symbol!)
odds.push(number); //If it isn't even append it to the empty list
}
return odds; // Return the new list
}
let example = removeEven([3, 2, 41, 3, 34]);
console.log('EXAMPLE:', example); //EXAMPLE: [ 3, 41, 3 ]
This approach starts with the first element of the array. If that current element is not even, it pushes this element into a new array. If it is even, it will move to the next element, repeating until it reaches the end of the array. In regards to time complexity, since the entire array has to be iterated over, this solution is in O(n)O(n).
Solution #2: Using filter() and lambda function
function removeEven(arr) {
return arr.filter((v) => v % 2 != 0);
}
console.log(removeEven([3, 2, 41, 3, 34]));
This solution also begins with the first element and checks if it is even. If it is even, it filters out this element. If not, skips to the next element, repeating this process until it reaches the end of the array.
The filter function uses lambda or arrow functions, which use shorter, simpler syntax. The filter filters out the element for which the lambda function returns false. The time complexity of this is the same as the time complexity of the previous solution.
Stack: Check for balanced parentheses using a stack
Problem statement: Implement the isBalanced() function to take a string containing only curly {}, square [], and round () parentheses. The function should tell us if all the parentheses in the string are balanced. This means that every opening parenthesis will have a closing one. For example, {[]} is balanced, but {[}] is not.
Input: A string consisting solely of (, ), {, }, [ and ]
exp = '{[({})]}';
Output: Returns False if the expression doesn't have balanced parentheses. If it does, the function returns True.
True
To solve this problem, we can simply use a stack of characters. Look below at the code to see how it works.
index.js
Stack.js
"use strict";
module.exports = class Stack {
constructor() {
this.items = [];
this.top = null;
}
getTop() {
if ( this.items.length == 0 )
return null;
return this.top;
}
isEmpty() {
return this.items.length == 0;
}
size() {
return this.items.length;
}
push( element ) {
this.items.push( element );
this.top = element;
}
pop() {
if ( this.items.length != 0 ) {
if ( this.items.length == 1 ) {
this.top = null;
return this.items.pop();
This process will iterate over the string one character at a time. We can determine that the string is unbalanced based on two factors:
- The stack is empty.
- The top element in the stack is not the right type.
If either of these conditions is true, we return False. If the parenthesis is an opening parenthesis, it is pushed into the stack. If by the end all are balanced, the stack will be empty. If it is not empty, we return False. Since we traverse the string exp only once, the time complexity is O(n).
Queue: Generate Binary Numbers from 1 to n
Problem statement: Implement a function findBin(n), which will generate binary numbers from 1 to n in the form of a string using a queue.
Input: A positive integer n
n = 3;
Output: Returns binary numbers in the form of strings from 1 up to n
result = ['1', '10', '11'];
The easiest way to solve this problem is using a queue to generate new numbers from previous numbers. Let's break that down.
index.js
Queue.js
"use strict";
module.exports = class Queue {
constructor () {
this.items = [];
this.front = null;
this.back = null;
}
isEmpty() {
return this.items.length == 0;
}
getFront() {
if ( this.items.length != 0 ) {
return this.items[ 0 ];
} else
return null;
}
size() {
return this.items.length;
}
enqueue( element ) {
this.items.push( element );
}
The key is to generate consecutive binary numbers by appending 0 and 1 to previous binary numbers. To clarify,
- 10 and 11 can be generated if 0 and 1 are appended to 1.
- 100 and 101 are generated if 0 and 1 are appended to 10.
Once we generate a binary number, it is then enqueued to a queue so that new binary numbers can be generated if we append 0 and 1 when that number will be enqueued.
Since a queue follows the First-In First-Out property, the enqueued binary numbers are dequeued so that the resulting array is mathematically correct.
Look at the code above. On line 7, 1 is enqueued. To generate the sequence of binary numbers, a number is dequeued and stored in the array result. On lines 11-12, we append 0 and 1 to produce the next numbers.
Those new numbers are also enqueued at lines 14-15. The queue will take integer values, so it converts the string to an integer as it is enqueued.
The time complexity of this solution is in O(n)O(n) since constant-time operations are executed for n times.
Linked List: Reverse a linked list
Problem statement: Write the reverse function to take a singly linked list and reverse it in place.
Input: a singly linked list
LinkedList = 0->1->2->3-4
Output: a reverse linked list
LinkedList = 4->3->2->1->0
The easiest way to solve this problem is by using iterative pointer manipulation. Let's take a look.
index.js
LinkedList.js
Node.js
"use strict";
const Node = require( './Node.js' );
module.exports = class LinkedList {
constructor() {
this.head = null;
}
//Insertion At Head
insertAtHead( newData ) {
let tempNode = new Node( newData );
tempNode.nextElement = this.head;
this.head = tempNode;
return this; //returning the updated list
}
isEmpty() {
return ( this.head == null );
}
//function to print the linked list
printList() {
if ( this.isEmpty() ) {
console.log( "Empty List" );
return false;
} else {
let temp = this.head;
while ( temp != null ) {
process.stdout.write( String( temp.data ) );
process.stdout.write( " -> " );
temp = temp.nextElement;
We use a loop to iterate through the input list. For a current node, its link with the previous node is reversed. then, next stores the next node in the list. Let's break that down by line.
- Line 22- Store the
currentnode'snextElementinnext - Line 23 - Set
currentnode'snextElementtoprevious - Line 24 - Make the
currentnode the newpreviousfor the next iteration - Line 25 - Use
nextto go to the next node - Line 29 - We reset the
headpointer to point at the last node
Since the list is traversed only once, the algorithm runs in O(n).
Tree: Find the Minimum Value in a Binary Search Tree
Problem statement: Use the findMin(root) function to find the minimum value in a Binary Search Tree.
Input: a root node for a binary search tree
bst = { 6 -> 4,9 4 -> 2,5 9 -> 8,12 12 -> 10,14}where parent -> leftChild,rightChild
Output: the smallest integer value from that binary search tree
2
Let's look at an easy solution for this problem.
Solution: Iterative findMin( )
This solution begins by checking if the root is null. It returns null if so. It then moves to the left subtree and continues with each node's left child until the left-most child is reached.
index.js
BinarySearchTree.js
Node.js
'use strict';
const Node = require('./Node.js');
module.exports = class BinarySearchTree {
constructor(rootValue) {
this.root = new Node(rootValue);
}
insert(currentNode, newValue) {
if (currentNode === null) {
currentNode = new Node(newValue);
} else if (newValue < currentNode.val) {
currentNode.leftChild = this.insert(currentNode.leftChild, newValue);
} else {
currentNode.rightChild = this.insert(currentNode.rightChild, newValue);
}
return currentNode;
}
insertBST(newValue) {
if (this.root == null) {
this.root = new Node(newValue);
return;
}
this.insert(this.root, newValue);
}
preOrderPrint(currentNode) {
if (currentNode !== null) {
console.log(currentNode.val);
this.preOrderPrint(currentNode.leftChild);
}
}
};
Graph: Remove Edge
Problem statement: Implement the removeEdge function to take a source and a destination as arguments. It should detect if an edge exists between them.
Input: A graph, a source, and a destination
Output: A graph with the edge between the source and the destination removed.
removeEdge(graph, 2, 3);
The solution to this problem is fairly simple: we use Indexing and deletion. Take a look
index.js
Graph.js
LinkedList.js
Node.js
const LinkedList = require('./LinkedList.js');
const Node = require('./Node.js');
module.exports = class Graph {
constructor(vertices) {
this.vertices = vertices;
this.list = [];
let it;
for (it = 0; it < vertices; it++) {
let temp = new LinkedList();
this.list.push(temp);
}
}
addEdge(source, destination) {
if (source < this.vertices && destination < this.vertices) this.list[source].insertAtHead(destination);
return this;
}
printGraph() {
console.log('>>Adjacency List of Directed Graph<<');
let i;
for (i = 0; i < this.list.length; i++) {
process.stdout.write(`|${String(i)}| => `);
}
}
};
Since our vertices are stored in an array, we can access the source linked list. We then call the delete function for linked lists. The time complexity for this solution is O(E) since we may have to traverse E edges.
Hash Table: Convert Max-Heap to Min-Heap
Problem statement: Implement the function convertMax(maxHeap) to convert a binary max-heap into a binary min-heap. maxHeap should be an array in the maxHeap format, i.e the parent is greater than its children.
Input: a Max-Heap
maxHeap = [9, 4, 7, 1, -2, 6, 5];
Output: returns the converted array
result = [-2, 1, 5, 9, 4, 6, 7];
To solve this problem, we must min heapify all parent nodes. Take a look.
function minHeapify(heap, index) {
const left = index * 2;
const right = index * 2 + 1;
let smallest = index;
if (heap.length > left && heap[smallest] > heap[left]) {
smallest = left;
}
if (heap.length > right && heap[smallest] > heap[right]) smallest = right;
if (smallest != index) {
const tmp = heap[smallest];
heap[smallest] = heap[index];
heap[index] = tmp;
minHeapify(heap, smallest);
}
return heap;
}
function convertMax(maxHeap) {
for (var i = Math.floor(maxHeap.length / 2); i > -1; i--) maxHeap = minHeapify(maxHeap, i);
return maxHeap;
}
var maxHeap = [9, 4, 7, 1, -2, 6, 5];
console.log(convertMax(maxHeap));
We consider maxHeap to be a regular array and reorder it to accurately represent a min-heap. You can see this done in the code above. The convertMax() function then restores the heap property on all nodes from the lowest parent node by calling the minHeapify() function. In regards to time complexity, this solution takes O(nlog(n))O(nlog(n)) time.